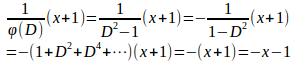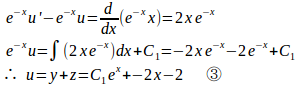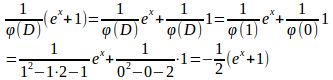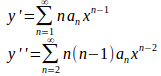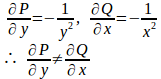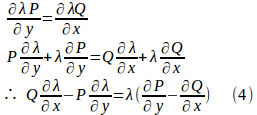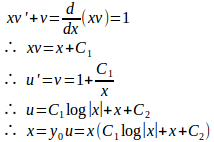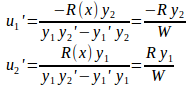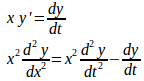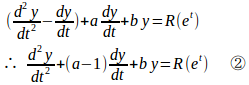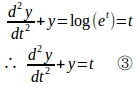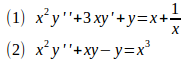第21回 ベクトルを用いた連立常微分方程式の解法 [ネコ騙し数学]
第21回 ベクトルを用いた連立常微分方程式の解法
次の連立常微分方程式について考える。
この連立常微分方程式の解がであるとし、①と②に代入すると、
だから、これで両辺を割ることができて、
という連立方程式が得られる。
行列と(縦)ベクトル
を用いて③式を書き換えると、
さらに、これを単位行列E
を導入し、式を変形すると、
すなわち、
もし、行列A−rEが逆行列をもつならば、
となり、連立方程式③の解はa=b=0になってしまうので、a=b=0以外の解をもつためには、行列A−rEが逆行列をもたない、つまり、その行列式
![]()
がでなければならない。
よって
そして、③式の第1式から、
r=1のとき
で、a=1にすると
r=3のとき
となる。
以上のことから、と
が基本解のセット、すなわち、この微分方程式の解ベクトルで、この微分方程式の解は
このように、行列の固有値とその固有ベクトルを用いて連立常微分方程式を解くこともできるというお話。
このあたりの正確な議論をするためには、線形代数の基礎知識を必要とするので、こういうふうに解くこともできるのだということ。
この連立微分方程式は、次のように簡単に解くことができる。
①+②
①−②
④+⑤
④−⑤
そして、ここで
とおけば、
となり、同じ結果が得られる。
二元連立常微分方程式ならば行列の固有値とその固有ベクトルを用いた解法を使う必要はないけれど、三元、四元、それ以上の多元連立方程式を扱う場合、行列とベクトルを用いた解法は強力なツールになる。
問題 次の連立微分方程式を解け。
【解】
とすると、
a、bがa=b=0以外の解をもつためには
固有ベクトルは、①の第1式より、
r=1のとき
r=5のとき
(解答終)
【別解】
連立微分方程式が
の形に書き換えるとすると、
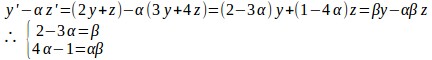
これを解くと、。
α=−1、β=5のとき
α=1/3、β=1のとき
①−②
①+3×②
ここで、
とおけば、
【別解2】
とおくと、微分方程式は
zを消去するために、①にD−4をかけると、
![]()
これに②を加えると、
よって、この特性方程式は
したがって、が基本解で
また、第1式より
![]()
よって、
(解答終)
第20回 連立常微分方程式の解法 [ネコ騙し数学]
第20回 連立常微分方程式の解法
例題 次の連立微分方程式を解け。
【解】
①から未知関数zを消去するために①を微分すると、
これに②のz'=y+xを代入すると、
非同次方程式を解くために、③の右辺=0とした同次形方程式
を解く。
上の同次形方程式の特性方程式は
したがって、④の基本解はであり、④の一般解は
また、④の特殊解は
ここで
したがって、③の一般解は
また、①より
よって、連立常微分方程式の解は
(解答終)
上の解答では、③の特殊解を用いるのに演算子Dを用いたが、特殊解をAx+Bと予測し、これを③式に代入すると、y''=0だから、
と特殊解を求めてもよい。
【別解】
①と②を足すと、
ここで、u=y+zとおくと、
両辺にをかけると、
①と②の差をとると
③と④をyとzについて解くと、
(解答終)
微分や積分という演算を含むけれど、普通の連立方程式の代入法、加減法のように解くことができる。
問題 次の連立微分方程式を解け。
【解】
(1) 第1式を微分すると、
第2式より
この特性方程式
したがって、この微分方程式の基本解は。
特殊解は
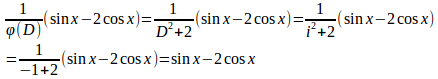
よって、
第1式より
(2) 第1式を微分し、第2式を用いると、
この微分方程式の特性方程式は
よって、基本解は。
特殊解は
よって、
また、第1式より
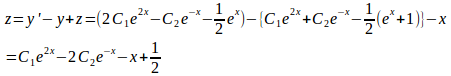
(解答終)
微分演算子を含む多項式は、Dを定数係数のように計算することができるので、これを用いて例題の微分方程式を次のように解くこともできる。
問題2 次の連立微分方程式を解け。
【解】
D×①
zを消去するために、上式に②を加えると、
よって、この微分方程式の基本解はで、特殊解は
したがって、
(以下略)
第19回 級数を用いた微分方程式の解法 [ネコ騙し数学]
第19回 級数を用いた微分方程式の解法
かりに次の微分方程式があるとする。
もしこの微分方程式の解が
と、べき級数で表され、さらに、項別微分が可能、すなわち、
であるとすれば、(1)式は
となり、べき級数の係数を比較すると
という漸化式が得られ、さらに初期条件y(0)=1より
したがって、漸化式から
となり、
が得られる。
(2)のべき級数(マクローリン級数)は、
であり、(1)の解と一致する。
ちなみに、(2)のべき級数の収束半径Rは、
参考までに、次の定理を。
定理
整級数の収束半径をR>0とすると、この整級数で定義された関数fは、−R<x<Rで微分可能で、項別微分が可能である。すなわち、
である。
問題1 次の微分方程式の解を求めよ。
【解】
とし、項別微分が可能であるとする。
だから、これを微分方程式に代入すると、
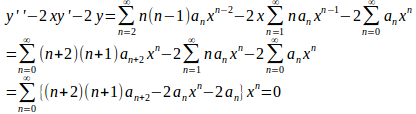
これがすべてのxについて成立するから、
また、初期条件より
したがって、
nが奇数のとき、すなわち、n=2m+1(m=0,1,2,・・・)のとき、
nが偶数のとき、すなわち、n=2mのとき
よって、
![]()
したがって、
(解答終)
問題2 次の微分方程式の与えられた初期値をもつべき級数解を、はじめの0でない3個まで求めよ。
【解】
とおくと、
初期条件y(0)=0よりa₀=0。
また、初期条件y(0)=0より
①と②を微分方程式に代入すると、
xとx²の項を比較すると、
したがって、
x³の項を比較すると、
よって、
(解答終)
同次関数とオイラーの定理 [ネコ騙し数学]
関数f(x,y)が任意の実数x、y、tに対して
が成り立つとき、f(x,y)をm次同次関数という。
fが1変数関数の場合は、
2変数以上の関数の場合は
である。
たとえば、
という関数があるとする。
このとき、
が成立するので、これは1次の同次関数である。
また、
とすると、
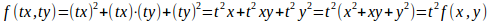
が成立するので、これは2次の同次関数である。
また、f(x,y)とg(x,y)を1次の同次関数とすると、
となるので、1次の同次関数の和は1次の同時関数である。
このことはほとんど明らかであるが、さらに、αを実数とすると、
が成立し、関数fの実数倍も1次の同次関数である。
問題1 f(x,y)をm次同次関数、すなわち、
が成り立つとき、次の問に答えよ。
(1)
(2) fがC¹級で
を満たすならば、fはm次同次関数である。
【解】
(1)
また、
だから、
よって、
t=1とすると、
である。
(2) とおきtで微分すると、
![]()
よって、φ(t)はtについて定数。
したがって、
(解答終)
問題1の(1)をオイラーの定理といい、(2)はオイラーの定理の逆である。
問題2
(1) m次同次関数z=f(x,y)において、とすると、
が成り立つことを示せ。
(2) (1)の結果を用いて、0次同次関数は、なる形をもつことを示せ。
【解】
(1)
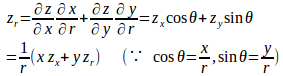
z=f(x,y)はm次同次関数だから、問題1より
したがって、
である。
(2) z=f(x,y)は0次同次関数だからm=0。
したがって、
したがって、zはだけの関数、つまり、y/xだけの関数となる。
よって、
(解答終)
なぜ、次の形の微分方程式を同次形というのか、その理由がわかってもらえるのではないだろうか。
第17回 積分因子2 [ネコ騙し数学]
第17回 積分因子2
問題1 微分方程式
について、次の問に答えよ。
【解】
λを微分方程式
の積分因子とすると、
は完全形。
したがって、
でなければならない。
(1) 積分因子λがt=x+yだけの関数
とすると、
①に代入すると、
C=1とすれば、
が得られる。
(2) 積分因子λがt=xyだけの関数
とすると、
①に代入すると、
C=1とすれば、
(3) 積分因子λがt=x²+y²だけの関数
であるとすると、
これを①に代入すると、
C=1とすれば、
を得る。
(解答終)
第17回 積分因子 [ネコ騙し数学]
第17回 積分因子
次の全微分方程式があるとする。
この全微分方程式は、
とおくと、
だから完全形ではない。
しかし、(1)式の両辺にxyをかけると
となり、P=x、Q=yとおくと、
が成立し、完全形の微分方程式にすることができる。
ちなみに、(2)式の解は
定義
完全形でない全微分方程式
に適当な関数λ(x,y)≠0をかけて得られる
が完全形であるとき、λ(x,y)をPdx+Qdy=0の積分因子または積分因数という。
先にあげた例だとxyは微分方程式(1)の積分因子である。
(3)式は完全形だから、
でなければならない。
そして、(4)式を解くことによって積分因子を求めることができる。
しかし、一般に偏微分方程式(4)を解くことは難しい。そこで、特別な場合を考えることにする。
λがxだけの関数の場合、
だから、(4)式は
となり、がxだけの関数であれば、積分因子は
と求まる。
同様に、がyだけの関数であれば、積分因子は
として求まる。
問題1 次の全微分方程式の積分因子を見つけ、一般解を求めよ。
【解】
(1) P=2xy、Q=y²–x² とすると、
したがって、積分因子は
![]()
微分方程式
の両辺に1/y²を掛けると、
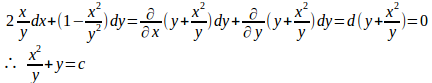
(2) P=x+y、Q=−xとおくと、
したがって、積分因子は
微分方程式
の両辺に1/x²を掛けると
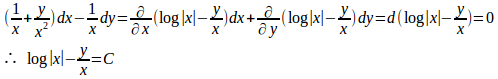
(解答終)
問題2 線形微分方程式
を変形して得られる
の積分因子を求めよ。
【解】
とおくと、
したがって、積分因子は
(解答終)
第16回 階数を下げる方法 [ネコ騙し数学]
第16回 階数を下げる方法
例題1 次の微分方程式を解け。
【解】
y'=pとすると、この微分方程式は
したがって、
(解答終)
問題1 次の微分方程式を解け。
ただし、aは定数。
【答】
例題2 次の微分方程式を解け。
【解】
p=y'とおくと、微分方程式は
となる。
となるので、①は
両辺を2乗して、整理すると
(解答終)
例題3 次の微分方程式を解け。
【解】
この微分方程式は、y'=pとおき、
となるので、例題2と同様に
とすると、
(解答終)
例題3は、【解1】のように簡単に解けてしまうのだけれど、
とおくと、
が成立するので、F(y,y',y'')は(2次の)同次形であり、微分方程式
は同次形の微分方程式である。
このことに注目して、次のように解くことも可能である。
【別解】
とおくと、
両辺をxで微分すると、
したがって、①は
y≠0のとき
y=0は、C₂=0の場合なので、
【解答終】
問題2 次の微分方程式を解け。
【解】
これは同次形の微分方程式。
そこで、
とおくと、
①に代入すると、
y≠0のとき
y=0は、C₂=0の場合なので、
(解答終)
第15回 2階線形非同次微分方程式の解法2 [ネコ騙し数学]
第15回 2階線形非同次微分方程式の解法2
問題1 線形微分方程式
は、その同次方程式
の解y₀を知れば、
と置換することにより、v=u'のについての1階線形微分方程式に帰着されることを示し、これにより次の微分方程式を解け。
【解】
を①に代入すると、
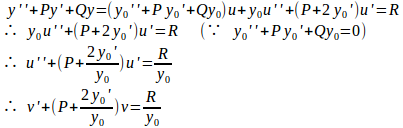
(1)
これは、
の場合だから、
よって、
(2)
これは、
の場合だから、
両辺にxを掛けると、
(解答終)
問題1の(1)、(2)ともにオイラー形の微分方程式なので、または
と変換して解くことができる。
この変換によって、
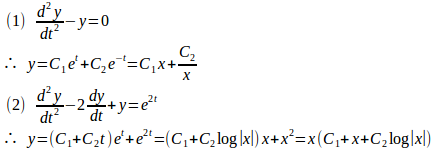
と解くことができる。
問題2 微分方程式
において、
とおくと、u(x)は
を満たすことを示せ。これを2階線形微分方程式の標準化という。
【解】
だから、y=uvを微分方程式に代入すると、
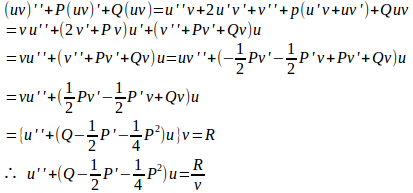
(解答終)
問題3 次の微分方程式を標準形に直して解け。
【解】
(1)
そこで、y=uvとおくとuの微分方程式は
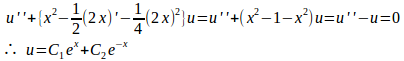
よって、
(2)
よって、
したがって、
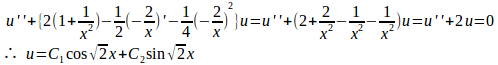
よって、
(解答終)
第14回 2階線形非同次微分方程式の解法 [ネコ騙し数学]
第14回 2階線形非同次微分方程式の解法
2階線形非同次常微分方程式
に関して次のことが成り立つ。
同次線形微分方程式
の基本解をy₁,y₂、ロンスキアンWを
とすれば、
は(1)の1つの特殊解である。
問題1 同次方程式(2)の一般解の任意定数C₁、C₂をそれぞれ未知関数u₁、u₂で置き換えた
が非同次方程式(1)の解となるようにu₁、u₂を定めることにより(3)で定めた特殊解を導け。
【解】
![]()
だから、
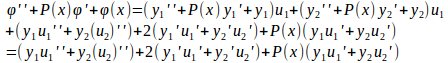
そこで、
となるようにu₁、u₂を定める。
の両辺をxで微分すると、
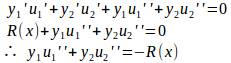
よって、
となり、φは非同次方程式
の解である。
①の連立方程式をについて解くと、
したがって、
よって、
(解答終)
問題2 次の微分方程式を解け。
【解】
(1) 同次方程式y' –y'–2y=0の基本解はなので、この一般解は
そこで、とおき、
(3)式を用いて、非同次方程式
の特殊解を求めると、
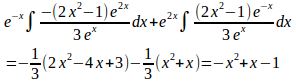
よって、①の一般解は
(2) (1)の結果を利用すると、y''–y'–2=cosxの特殊解は
よって、一般解は
(3) 同次方程式の基本解は、
より、であり、この一般解は
である。
式(3)より、非同次方程式
の特殊解は
![]()
したがって、非同次方程式①の一般解は
(解答終)
問題2の(2)の特殊解は
と予想できるので、
を①に代入し、
と、特殊解を求めたほうが簡単。
第13回 オイラー方程式 [ネコ騙し数学]
第13回 オイラー方程式
オイラー形の微分方程式の一般形は
である。
とおくと、
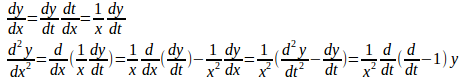
同様に
となるので、(1)は定数係数のn階線形常微分方程式に変換することができる。
問題1
は、と置換することにより、y、tの定数係数線形微分方程式になることを示し、これにより次の微分方程式を解け。
【解】
とし、両辺をtで微分すると、
よって、
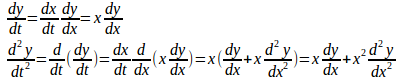
したがって、
これを①に代入すると、
(1) a=1、b=1、R(x)=logxの場合だから、
同次方程式
の一般解は
y=tは③の特殊解だから、③の一般解は
(2) a=−1、b=1、R(x)=x²の場合だから、
同次方程式
の特性方程式
の解は、λ=1で重根。
したがって、同次形の一般解は
は④の特殊解だから、④の一般解は
(解答終)
問題2 次の微分方程式の一般解を求めよ。
【解】
(1) x>0のとき、とおくと、
だから、微分方程式は
同次形方程式
の特性方程式
だから、同次方程式の一般解は
①の特殊解y₀は
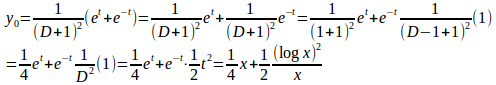
x<0のときも同様の関数になる。
(2) x>0のとき、とおくと、
したがって、微分方程式は
同次方程式
の特性方程式は
したがって、同次方程式の一般解は
①の特殊解は
x<0のときも同様。
よって、
(解答終)