番外編 円の方程式 [ネコ騙し数学]
番外編 円の方程式
§1 円の方程式
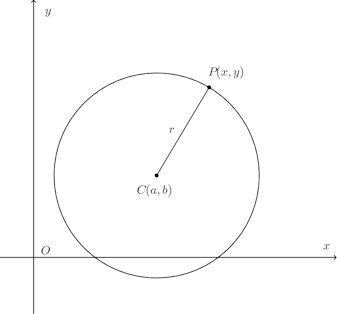
(1) 円の基本形CとPがxy平面上にある、その座標がそれぞれ(a,b)、(x,y)であるとすると、この円の方程式は、二点間の距離の公式(三平方の定理)より
特に、円の中心Cが(a,b)=(0,0)、つまり、原点であるとき、円の方程式は
繰り返し書くけれど、中心C(a,b)で半径rの円の方程式は
(2) 円の一般形
よって、l²+m²−4n>0のとき、②は中心
問題1 次の円の方程式を求めよ。
(1) 中心が(1,2)で、点(5,0)を通る(2) 2点(4,-5)、(2,3)を結ぶ線分を直径とする円
(3) 3点A(-3,7)、B(4,6)、C(3,−1)を通る円【解】
円の半径をrとする。(1) 円の方程式は、①より
(別解)
半径rは(1,2)と(5,0)の2点間の距離に等しい。よって
(2) 円の中心は2点(4,-5)、(2,3)を結ぶ線分の中点。
よって、円の中心(a,b)は
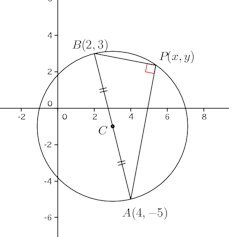
(別解)
この円の方程式は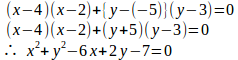
だケロ!!
(x₁,y₁)、(x₂,y₂)を両端とする円の方程式は
なぜならば、A(x₁,y₁)、B(x₂,y₂)、P(x,y)とすると、AP⊥BPだから
(3) 解くの面倒くさいにゃ。
円の方程式を
問題2 次の方程式があらわす円の中心、および、半径を求めよ。
(1) x²+y²−6x+4y−12=0(2) x²+y²=6x
【解】(1) x²+y²−6x+4y−12=0の平方完成をする。
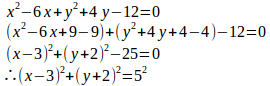
よって、中心(3,−2)、半径5の円。
(2) x²+y²=6xだから
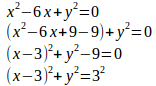
よって、中心(3,0)、半径3の円。
§2 円と直線
(1) 直線と点の距離直線ax+by+c=0と点(x₁,y₁)の距離dは
(2) 円と直線
円の半径をr、円の中心と直線の距離をdとするとき、(ⅰ) r<dならば交点0
(ⅱ) r=dならば交点1(接点)(ⅲ) r>dならば交点2
になる。これらの知識を使って円と直線の交点の数の判別をしてみることにする。
問題3 x²+y²=4とy=ax−3との共有点の個数は、実数aの値によってどう変わるか。
【解】
d>2のとき
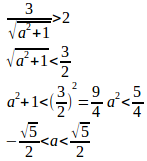
d=2のとき
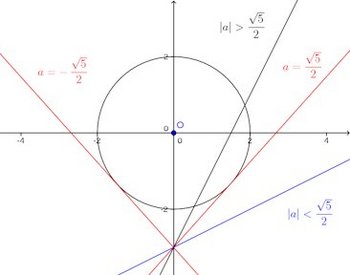
タグ:初等幾何
2016-06-15 12:26
nice!(0)
コメント(0)
トラックバック(0)





コメント 0