第３回 定積分の性質１

第３回　定積分の性質１

リーマン和をもとに（定）積分を定義すると、高校で習った定積分の次の定理を証明することができる。

定理１

f(x)、g(x)が有界閉区間[a,b]で積分可能、λ、μが定数であるとき、λf(x)+μg(x)は[a,b]上で積分可能で、
　　

である。

【証明】

分割とを任意にとると、リーマン和は

　　

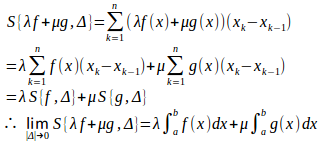
となり、λf(x)+μg(x)は[a,b]上で積分可能で、

　　

である。

（証明終了）

定理２

f(x)、g(x)は有界閉区間[a,b]で積分可能であるとする。このとき、

　　

ならば、

　　

である。

【証明】

分割とを任意にとると、仮定より

　　

であるから、
　　

f(x)、g(x)は[a,b]上で積分可能だから、｜Δ｜→0のとき

　　

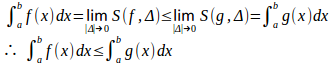
（証明終）

関数f、gが有界閉区間[a,b]上で連続であるとき、f=g、つまり、x∈[a,b]のすべてのxについてf(x)=g(x)でなく、

　　

であるとき、

　　

になるけれど、単に積分可能であるときは、等号は外せないことに注意。

 

たとえば、[0,1]で定義されたf(x)=0と

　　

の積分を考えればよい。

このとき、f≠gで、f(x)≦g(x)という条件を満たしているが、

前回の問題２で示したように、gは[0,1]で積分可能でその値は

　　

だから、

　　

である。

また、fは[a,b]上で積分可能で、x∈[a,b]のすべてのxについてf(x)≧0のとき、

　　

ならば、x∈[a,b]でf(x)=0も言えない。

 

定理３

有界な関数f、gが有界閉区間[a,b]の有限個の点を除き、f(x)=g(x)であるとする。このとき、fが[a,b]上で積分可能ならば、gも[a,b]上で積分可能で、

　　

が成り立つ。

【証明】

x=dを除いてf(x)=g(x)である関数g(x)を考え、

　　

とすると、φ(x)は[a,b]上で積分可能で、

　　

したがって、定理１より

　　

も[a,b]上で積分可能で、

　　

になる。

次に、を除いてf(x)=g(x)である関数g(x)を考える。

　　

とおき、

　　

とおくと、は[a,b]上で積分可能で、

　　

である。
　　

とおくと、

　　

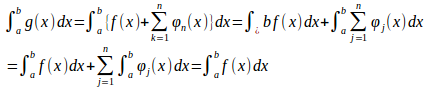
（証明終）

定理３より、たとえば、[0,3]で定義される

　　

という関数f(x)は[0,3]で積分可能であり

　　

である。

タグ：微分積分 定積分