第15回 2変数関数の極値の計算例 [ネコ騙し数学]
第15回 2変数関数の極値の計算例
偏微分を用いて2変数関数の極値を求める前に、極値に関する定理を再掲する。
定理15
関数f(x,y)が偏微分可能なとき、点(a,b)で極値を取るならば
である。
定理16 (極値の判別式)
f(x,y)は領域DでC²級の関数とする。(a,b)をf(x,y)の停留点とし
とおくとき、次のことが成り立つ。
(ⅰ) D>0のとき
ならば、f(x,y)は点(a,b)で極小、
ならば、f(x,y)は点(a,b)で極大となる。
(ⅱ) D<0のとき、f(x,y)は点(a,b)で極大でも極小でもない。
(ⅲ) D=0のとき、2階の偏微分係数だけからは判定できない。
なお、定理16に登場する停留点とは、である点を停留点のことである。
問題 次の関数の極値を求めよ。
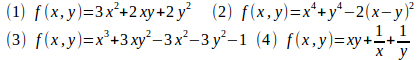
【解】
(1) より、停留点は(0,0)である。
だから
。
したがって、f(x,y)は(0,0)で極小で、f(0,0)=(0,0)が極小値である。
(2)
①と②を加えると
y=−xを①に代入すると、
よって、停留点は(0,0)、(√2,−√2)、(−√2,√2)である。
(x,y)=(√2,−√2)、(−√2,√2)のときだから
となるので極小、極小値は−8。
(0,0)のとき、D=0となり、2階偏微分係数を用いた極値の判定は出来ない。
したがって、(0,0)は極値ではない。
(3)
したがって、停留点は
②よりy=0、x=1。
y=0を①に代入すると、x²–2x=x(x–2 )=0より、x=0、2。
x=1を①に代入すると、y²–1=(y+1)(y–1)=0よりy=±1。
よって、停留点は(0,0)、(2,0)、(1,1),(1,−1)。
よって、(0,0)のとき、だから
となり、f(x,y)は(0,0)で極大、極大値はf(0,0)=−1になる。
(2,0)のとき、だから、f(x,y)は(2,0)で極小、極小値はf(2,0)=−5。
(1,1)、(1,−1)のとき、だから、極値ではない。
(4)
したがって、
②より
これを①に代入すると、
②にy=1を代入すると、x=1。
したがって、停留点は(1,1)。
よって、f(x,y)は点(1,1)で極小で、極小値はf(1,1)=3である。
(解答終)
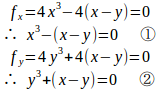
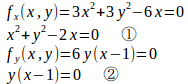
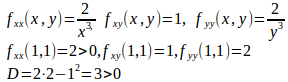




コメント 0