第20回 ラグランジュの未定乗数法 [ネコ騙し数学]
第20回 ラグランジュの未定乗数法
定理 (ラグランジュの未定乗数法)
関数φ(x,y)は点(a,b)の近傍でC¹級でφ(a,b)=0で、(a,b)は特異点でないとする。このとき、φ(x,y)=0の条件のもとでf(x,y)が点(a,b)で極値をとり、かつ全微分可能ならば、ある定数λがあって、次が成り立つ。
![]()
【証明】
点(a,b)は特異点でないので、または
。
いま仮にとすると、このとき、陰関数定理よりφ(x,y)=0はx=aの近傍でb=ψ(a)でC¹級な陰関数y=ψ(x)が存在する。
とおくと、g(x)はx=aで極値をとるからg'(a)=0。
また、
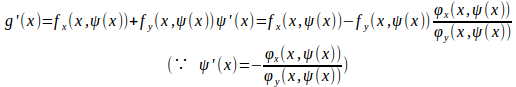
だから、
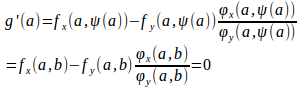
ここで、
とおくと、
(証明終)
問題1 x²+y²=1のとき、f(x,y)=x+yの最大値、最小値をと求めよ。
【解】
曲線φ(x,y)=x²+y²–1= 0は有界閉集合で、f(x,y)は連続だから最大値、最小値をもつ。
だから
となるのは(x,y)=(0,0)であるが、φ(0,0)=−1だから、φ(x,y)は特異点をもたない。
このとき、f(x,y)の最大値、最小値は極値だから、ラグランジュの未定乗数法より
とおくと、極値を取る点では
でなければならない。
λ≠0だから、①と②より
③に代入すると、
よって、
したがって、最大値は
最小値は
である。
(解答終)
【別解1」
x²+y²=1だから、x=cosθ、y=sinθ(0≦θ<2π)とおくと、三角形の合成公式より
よって、
θ=π/4、すなわち、x=y=1/√2のときに最大で最大値は√2で、
θ=5π/4、すなわち、x=y=−1/√2のときに最小で最小値は−√2である。
(別解1終)
【別解2】
x+y=kとおくと、直線x+y=kが円x²+y²=1に接するときに、kは最大、最小になる。
これは、原点と直線x+y–k=0の距離=1のときだから、
(別解2終)
問題2 4x²+y²=4の条件のもとで、f(x,y)=x+yの極値を求めよ。
【解】
曲線4x²+y²=4は有界閉集合で、f(x,y)は連続だからこの有界閉集合で最大値、最小値をもつ。
φ(x,y)=4x²+y²–4=0とおくと、だから、
となる点は(x,y)=(0,0)であるが、φ(0,0)=−1≠0なので、φ(x,y)=0は特異点をもたない。
ラグランジュの未定乗数法より
とおくと、
λ≠0だから、①と②より
③式に代入すると、
よって、
したがって、(x,y)=(1/√5,4/√5)のときにfは極大で極大値は√5、(x,y)=(−1/√5,−4/√5)のときにfは極小で極小値は−√5である。
(解答終)
【別解】
直線x+y=kが楕円4x²+y²=4に接するときにkは最大・最小。
y=k–xとおき、4x²+y²=4に代入すると、
(別解終)
問題3 x³+y³=3xyの条件のもとでf(x,y)=x²+y²の極値を求めよ。
【解】
φ(x,y)=x³+y³–3xy=0とおくと、 だから、(x,y)=(0,0)は特異点。
f(x,y)=x²+y²は非負だから(x,y)=(0,0)のときにf(0,0)=0で、このときに極小である。
(x,y)≠(0,0)とする。
ラグランジュの未定乗数法より
とおくと、
①、②より
x=yのとき、x³+y³=3xyより
陰関数定理より(x,y)=(3/2,3/2)でだから、x=2/3の近傍でyはxの関数である。
極値の判定をするために、f(x,y)=x²+y²とx³+y³=3xyをxで微分すると、
![]()
よって、(x,y)=(3/2,3/2)のとき
③と④の両辺をxで微分すると、
よって、(x,y)=(3/2,3/2)のとき、⑤式より
となり、(x,y)=(3/2,3/2)のとき、fは極大で、
x+y+xy=0のとき、x³+y³=3xyより
x+y=0とx³+y³=3xyより(x,y)=(0,0)。
以上のことより、(x,y)=(0,0)のとき、f(x,y)は極小で、極小値は0。
(x,y)=(3/2,3/2)のとき、f(x,y)は極大で、極大値は9/2。
(解答終)
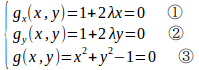
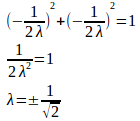
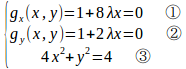
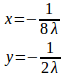
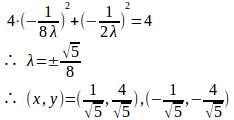
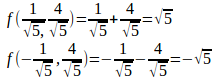
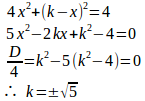
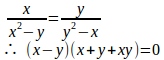
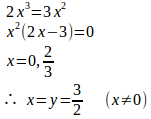
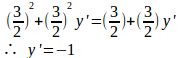
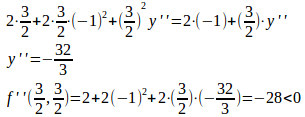
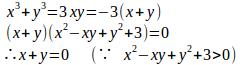




コメント 0