無限遠点とリーマン球面

無限遠点とリーマン球面

 

無限遠点

１次関数が

　　

の場合、z=0に対応する点はw平面に存在しない。この例外を除外するために無限遠点∞を導入し、次のように定義することにする。

w=1/zにおいて、点zが原点であるとき、その像はw平面上の∞であり、z平面の∞の像はw平面の原点である。

無限遠点∞は複素平面の原点から有限の距離になく、複素平面上をどの方向に進んでも原点からの距離が限りなく大きくなると、∞という１点に到達する。

さらに、∞を含む演算を次のように定義する。

　　

無限遠点∞は、微積分の無限大∞とは異なるので注意が必要である。

 

R>0のとき、｜R｜<zを満足する集合に無限遠点∞を加えたもの点集合をR近傍といい、いろいろなRに対する∞のR近傍を総称して∞の近傍といい、記号やなどで表す。

複素数列が任意のR>0に対して、適当な正の整数Nが存在し、

　　

であるとき、数列は∞に発散するといい、

　　

と書く。

なお、微積分で使われる無限大∞と無限遠点∞を区別するために、上式では無限大∞を＋∞で表している。

この定義は、のときと定義することと同じである。

 

複素球面（リーマン球面）

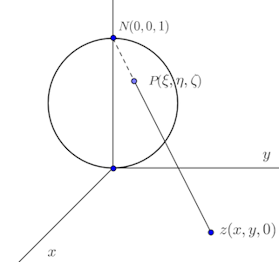複素平面上の原点Oに接する半径1の球面をつくり、Oを通る直径の他端をNとする（右図参照）。複素平面上の任意の点zとNを結ぶ直線はN以外のただ１点Pと交わる。逆に球面上のNと異なる任意の点Pを結ぶ直線は複素平面とただ１点で交わる。複素平面上の点zが原点から限りなく離れるとき、球面上の対応する点PはNに近づく。したがって、無限遠点∞に対応する点はNである。

このように考えたときの球面を複素球面（リーマン球面）といい、この球面上の点は∞を含めた複素平面と１対１に対応する。

Nの座標を(0,0,1)、Pの座標を(ξ、η、ζ)とするとき、

　

より

　　

という対応関係にある。

 

 

問　複素平面上の次の点は、リーマン球面のどの点にうつされるか。

【解】

（１）　式（２）により

　　

 

（２）　式（２）より

　　

 

 

（３）　式（２）より

　　

（解答終）