［内点方程式から境界方程式へ（ラプラス型）］

［内点方程式から境界方程式へ（ラプラス型）］

 

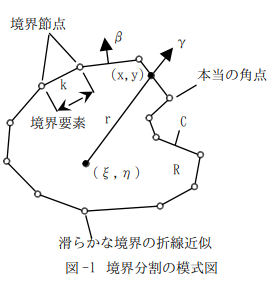
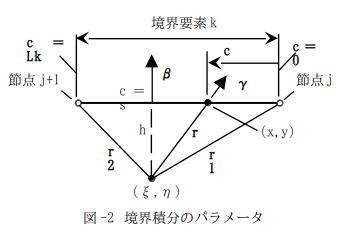
　前回までで内点方程式の境界積分公式を与える事ができました。同様に境界方程式の境界積分公式も作れるはずです。境界方程式では、基本解の特異点(ξ，η)は境界節点j＝1，2，・・・のどれかと一致します。そこで、(ξ，η)が最初から節点jやj+1と一致した図-2を考え、最初から(ξ，η)を境界上において積分計算を実行すれば良い訳です。それは実行可能ですが、初めから積分計算をやり直す事にもなります(^^;)。

　それならばという事で、今までの結果を再利用するという手があります。つまり前回までの結果で(ξ，η)が節点jやj+1に近づく極限を試す、という方法です。これは上手く行く上に、境界要素法に関わるある種の曖昧さの一つを解消できます。

 

　図-2の(ξ，η)が節点j+1に近づく極限を考えます。これはr₂→0という事なのでr₂＝εと表し、またγ₂がεの方向である事を明示するためにγ^(j+1)と書く事にすると、容易に（図をにらむだけ(^^)）、

　　

を導けます。これらの条件を考慮すると、前回の積分公式の極限は、

　　

を使って、

　　　
　　

 　　

 　　

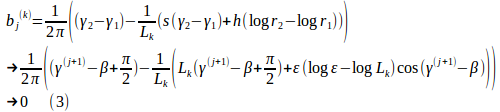
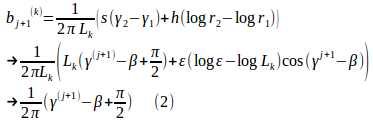
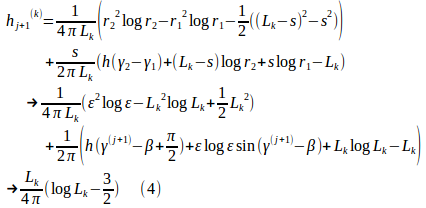
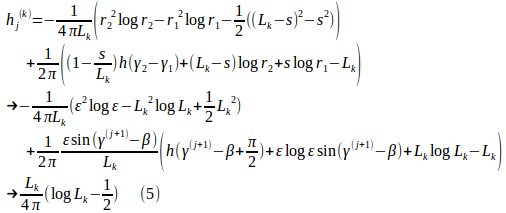
　同様に(ξ，η)→節点jでは、r₁＝ε，γ₁＝γ^(j)と表す事にして、

　　

なので、

　　

を得ます。

　これらを、［境界積分の積分部品（ラプラス型）］の最後のボトムアップ公式、

　　

 に代入すれば要素k上で、境界方程式の境界積分は、

　(ξ，η)→節点j+1の時：

　　

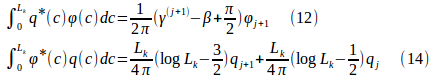
　(ξ，η)→節点jの時：

　　

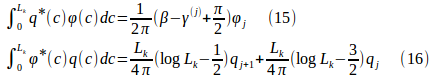
となります。

 

　注目は次です。以上の計算は、基本解の特異点を図-1の解析領域Rの内点として、(ξ，η)→節点j，j+1とした状況なので、内点方程式、

　　

の(ξ，η)→節点j，j+1の極限を取った状況です。式(17)の境界積分では要素kだけでなく、全ての要素の積分値を足すので、要素k上の積分値には必ずその隣の要素k+1での値も足されます。

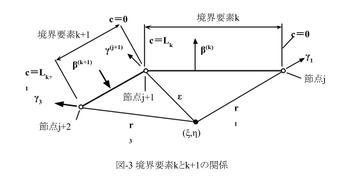
　式(17)左辺において、節点j+1を共有する要素kと要素k+1に注目します（図-3）。図-3で(ξ，η)が節点j+1に近づいた時のψ_j+1の項をまとめます。

 

　式(12)，(15)と図-3の記号を使って、

　　

 

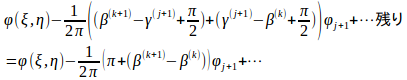
　ここにβ^(k+1)とβ^(k)は、要素k+1と要素kの外法線方向である事の明示です。

　(ξ，η)→節点j+1でした。従って、ψ(ξ，η)→ψ_j+1です。

　　

になります。

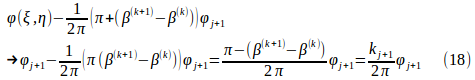
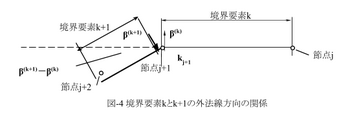
　ところが図-4に示すように、要素k+1は節点j+1からj+2にいたる線分で、その方向はβ^(k+1)＋π/2，要素kは節点jからj+1にいたる線分で方向はβ^(k)＋π/2。よって(β^(k+1)－β^(k))は、要素k+1と要素kの方向差です。図-4からπ－(β^(k+1)－β^(k))は、節点j+1の内角k_j+1となり、式(18)が得られます。

　この意味するところは、内点方程式(17)で(ξ，η)を境界に近づけたら、内点方程式は境界方程式、

　　

に化けたという事です。

　境界要素法の普通の定式化では、境界上でのデルタ関数の再評価で式(18)を導くので、(18)は(17)と無関係に不連続に成り立つように見えますが、ちゃんと積分してやれば、内点方程式から境界方程式へちゃんと連続的に移行できるのがわかります。数学ってなんて正直！(^^)。

　もっとも内点方程式から境界方程式への移行には式(1)が必要で、この計算はコンピュータには無理ですから、計算プログラム上は人間が式を使い分けてやる必要はあります(^^;)。

 

　これで計算準備はほとんど整いました。残ったのは式(17)，(18)右辺の領域積分項ですが、これは比較的簡単に扱えるので後回しにします。次にやる事は、数値計算用の境界方程式を組立てです。

 

※

　ここまでの内容を日本で最初に論文にしたのは、静電場解析にラプラス型の境界要素法を応用した、北大電気工学科の先生です（1980年代）。先生の名前は忘れましたが、2次元境界要素法，解析的積分あたりでググれば（かつ幸運なら）、その論文なんかにヒットするかも知れません。この先生はさらに、3次元領域表面を3角形メッシュで離散化した場合の、ラプラス型境界要素法の境界積分の解析的積分公式も与えています。いずれにしろ、「岩波数学公式集ゅう～～！」・・・です(^^)。

タグ：数値解析 境界要素法