第10回 微分と接線 [ネコ騙し数学]
第10回 微分と接線
『接線なんかやらなくてもいいかな』と思ったのですが、やっぱ、やらないわけにはいかないんだろうな。
図を作んなきゃいけないので、できたらやりたくないんだけど(^^ゞ
ある本(ネムネコが持っている本の一冊)の接線の定義
「yがaで微分可能なとき、y=f(x)のグラフ上の点P(a,f(a))を通る直線
をPにおける接線といい、Pで接線に直交する直線を法線という。」
この定義だと、ちょっとまずいんでしょうかね~。
これを微分すると、
となります。
この式を見るとわかりますけれど、x=±1で微分不可能になって、「x=±1で円の接線は存在しない(?)」となってしまう。
ですが、x=±1は間違いなく原点を中心とする単位円の接線。
「おいおい、この問題をどうするんだ」!!
悪知恵を働かせて逃げようとするならば、
だから、
これで許してもらえる?
それとも、
”「微分可能なとき」と書いてあるじゃないですか”と突っぱねる?
どうせ、ネコ騙しだし(^^ゞ
これで終わってしまうのなんですし、すこし問題でも解いてみますか。
【問題】
曲線
(1)曲線上の(3,-2)における接線の方程式を求めよ。
(2)傾きが2であるこの曲線の接線の方程式を求めよ。
【解答】
よって、接線の方程式は
(2)曲線上の傾き(微分係数)が2の点のx座標をaとすると、
a=0の時のy座標はf(0)=1
a=4の時のy座標は
と
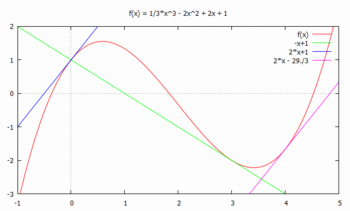
少し見にくいですが、グラフは
この勢いに乗って、さらにもう一つ。
【問題】 曲線![]() に、点(3,1)から引いた接線の方程式を求めよ。
に、点(3,1)から引いた接線の方程式を求めよ。
【解答】
x=aにおける接線の方程式は、
だから、
これが点(3,1)を通るので
このaを②に入れて計算すると、
接線単独じゃ~、これといって面白くないし、早いけれど、今回はこれで店じまいしますか。
と思ったのですが、
前回の「平均値の定理」の復習をかねて、次の問題でも解いてみますか。
【問題】
ある区間においてf'(x)は微分することができて、![]() で、かつ方程式
で、かつ方程式![]() が実根をもつものとする。このとき、αをその区間の実根の近似値とすれば
が実根をもつものとする。このとき、αをその区間の実根の近似値とすれば![]() はαよりよい近似値となることを示せ。
はαよりよい近似値となることを示せ。
【解答?】
平均値の定理より
これ、大昔に出た某国立大学の理系の大学入試問題。
fが微分可能で、![]() といったような関数の差の形が出てきたら、「平均値の定理」が使えるということを憶えておくと、何かと便利ですよ。
といったような関数の差の形が出てきたら、「平均値の定理」が使えるということを憶えておくと、何かと便利ですよ。
たとえば、
だとすると、
という不等式を作ることができる。
ここで、
を使っています。
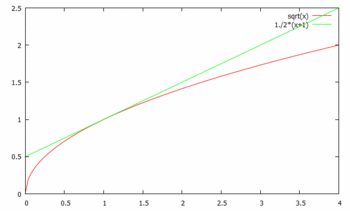
このグラフから、この不等式が成り立っていることがわかります。
そして、
はy=√xのx=1の接線で、x=1の近く(近傍)でy=√xのよい近似式になっているのであった。
接線と近似式の関係もいったし、平均値の定理の応用の仕方についても書いたし、これくらいでいいかな。
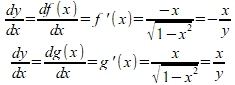
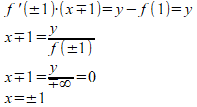
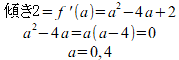
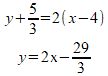
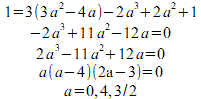
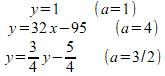
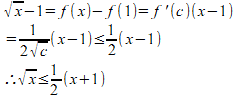




コメント 0