第２７回 ノルムと一様収束 [ネコ騙し数学]
第２７回 ノルムと一様収束
ノルムの話をする前に、上限について復習しますにゃ。
集合Sの上限とは次の二つの条件を満たすものにゃ。
１ ∀x ∈ S に対しx ≦ α
２ ∀ε > 0 に対しα – ε < x をみたすx ∈ S が存在する
この二つの条件を満たすαを上限といい、 sup S = α 、あるいは
と表わすんだケロ。
で、D定義された関数f、f：D →R、S ⊂ D とすると、f(S) は実数Rの部分集合だから、上限が定義できるんだケロ。
関数の上限の場合はちょっと表記が違って
と書くにゃ。関数f のS における上限とか、関数fのS上の上限とかいうにゃ。
というような関数があった場合、
といったふうに書くにゃ。ちなみにこの値は1 だにゃ。
この値が１になるのはわかるケロ？
で、どんなε > 0 をとっても
1 – ε < x
を満たすx ∈ [0, 1] に存在するから。
じゃぁ、定義域を0 < x < 1 、
としたとき、
の値は？
1だよね。
だから。
そして、1 より小さな上界は存在しないので。
厳密なことをいうと違うけれど、関数の最大値だと思ってくんな。「当たらずとも遠からず」ですから。
ノルム
D上で定義された有界な関数ｆのDにおけるノルムとは
で定義された実数のことである。
そして、一般に、Dを省いて
と略記するんだケロ。
何でこんなノルムなんてものを、突然、言い出したかというと、このノルムを使うと、関数列
の一様収束は、次のように言い換えられるからなんだケロ。
定理 D上で定義された関数列
に対し
が一様収束する必要十分な条件は
である。
この定理は上限の定義からほとんど明らかだから、証明しないケロ。
で、この定理を使うと、
例１ つぎのように定義される関数列をかんがえると、
の極限関数fはf(x) = 0 だケロ。
n を固定して考えると、関数
の最大値はx = 1 のときで、1/nだケロ。
よって、
となるケロ。
で、n → ∞にすると
になるから、この関数列は0 に一様収束することがわかるケロ。
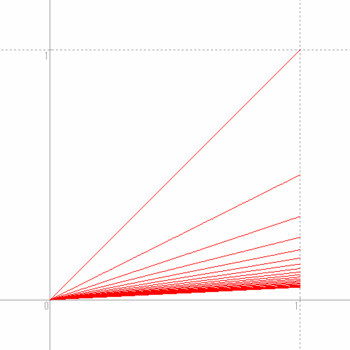
ちなみに、これは次のように収束してゆくにゃ。
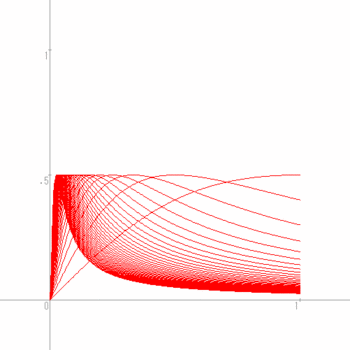
これに対して、第２５回の問題１のような
は、
極限関数f(x) = 0 となるので、この図からあきらかなように、
となり、これはn → 0 のとき、0 にならないにゃ。だから、一様収束じゃないことがわかるにゃ。
じゃぁ、第２４回の問題１
は・・・。
これはが有界じゃないから、そもそも、この定理は使えないにゃ。
この極限関数はf(x) = x だから
となり、
n を固定して、－∞ < x < ∞ で考えると、
になるので、ノルムを定義できないにゃ。
第２５回の例１
は、極限関数f(x) = 0
よって、
n → 0 とすると、これは0 になるケロ。だから、これは一様収束することがわかる。
まぁ、今回はこんな話にゃ。
こういうのは、感覚的にとらえた方がわかりやすいと思いますにゃ。
とf(x) の違いが一番大きいところの範囲の中に、
はすべて入るだろ。
で、
n → ∞にしたとおき、の上限（上限がピンとこないなら、最大値でいいわさ）が0 に限りなく近づけば、それは一様収束ってことだわさ。
コメント 0