第１５回 調和点列

第１５回　調和点列

同一直線上にA、B、P、Qがあって、P,QがABを同じ比に内分、外分、すなわち

　　AP:PB=AQ:QB

のとき、P、QはABを調和に分けるといい、４点A、B、P、Qはこの順に調和点列をなすという。

分かりづらいと思うのですが、A、B、P、Qは図のような位置関係になります。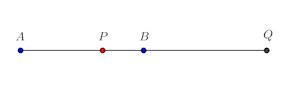

この図は、

　　AP:PB=AQ:QB=2:1

の場合について示したものです。

式を少し変形すると

　　

と言ったような関係が出てくるにゃ。

問題１　４点、A、B、C、Dが調和点列ならば

　　

であることを証明せよ。

【証明】

AB=b、AP=p、AQ=qとする。

そうすると、PB=b−p、BQ=q−bになる。

A、B、C、Dは調和点列をなしているので、②より

　　

となり、この逆数をとると

　　

（証明終わり）

前に調和平均について少し話したけれど、このことからbはpとqの調和平均になっていることが分かる。

第１０回と第１１回で次の定理を紹介したにゃ。

定理　△ABCにおいて∠A（またはその外角）の２等分線が対辺（またはその延長）で交わる点をDとすると、

　　BD:DC=AB:AC

である。

△ABCにおいて∠Aの２等分線とBCの交点をP、また、∠Aの外角の２等分線とBCの延長との交点をQとする。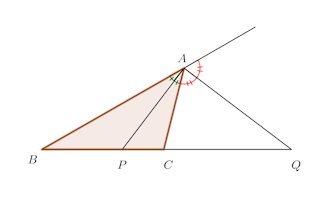

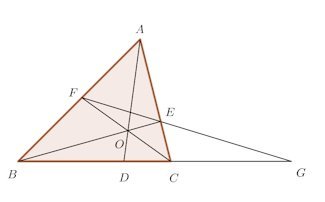
上の定理から、

　　

になるので、B、C、P、Qが調和点列である。

問題２　△ABC内に１点Oをとり、AO、BO、COが対辺と交わる点をそれぞれD、E、Fとする。

このとき、D、GはBCを調和に分けることを証明せよ。

【証明】

△ABCと点Oについてチュバの定理を用いると

　　

△ABCとFGについてメネラウスの定理を用いると

　　

よって

　　

だから、D、GはBCを調和に分ける。

（証明終わり）

タグ：初等幾何