ロピタルの定理 [ネコ騙し数学]
ロピタルの定理
平均値の定理には、コーシーの平均値と呼ばる次のものがある。
コーシーの平均値の定理
f(x)、g(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能、さらにg'(x)=0ならば
【証明】
h(x)は、[a,b]で連続、(a,b)で微分可能、かつ、h(a)=h(b)=0。
ロールの定理より
g'(x)はa<x<bでg'(x)≠0だから、g'(c)≠0。
よって、
(証明終わり)
この平均値の定理を使うと、次のロピタルの定理を証明することができる。
ロピタルの定理
f(a)=0、g(a)=0で、f(x)、g(x)がx=aを含む近傍で連続、x=a以外で微分可能とする。
x=aの近傍で、aとは異なる任意の数をxとすると、コーシーの平均値の定理より
仮定より、f(a)=0、g(a)=0だから
したがって、
(略証終わり)
感覚に訴えるかける証明で厳密なものではないけれど、ひとまず、これで納得していただけるのではないか。
このロピタルの定理は、0/0や∞/∞といった不定形の極限値を求める時に便利な定理である。
問題1 f(x)が連続な導関数をもつとき、次の極限を求めよ。
この問題では、x=aのとき、分子・分母ともに0で、0/0のタイプの不定形の極限。
ということで、ロピタルの定理が使える(かもしれない)。
問題2 次の極限を求めよ。
これは∞/∞の極限で、分子・分母ともに微分可能。
よって、ロピタルの定理より
(解答終わり?)
しかし、これはロピタルの定理の誤用。
−1≦cosx≦1だから、x−1≦x−cosx≦x+1。
また、次のような誤用もある。
問題3 次の極限を求めよ。
ロピタルの定理より
(解答終わり)
上の【解?】のどこがいけないかというと、
x=0のとき、cosx≠0で、そもそも、ロピタルの定理の前提条件を満たしていない!!そして、この極限は
このロピタルの定理は、この定理の理解不足による誤用が多いことで有名。
だから、この定理は極力使用は避けるべきで、極限を求める方法がどうしてもわからないときにのみ使用を限るべきだ。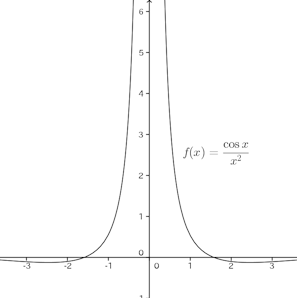




コメント 0