定積分と面積

定積分と面積

§１　定積分と面積

閉区間[a,b]で関数f(x)が連続、かつ、f(x)≧0であるとする。このとき、曲線y=f(x)とx軸およびx=a、x=bで囲まれた図形の面積をSとするとき、

　　

である。

閉区間[a,b]内の任意の点xをとり、区間[a,x]で曲線とx軸とで囲まれた部分の面積をS(x)とすると、S(x)はxに応じて定まる関数である。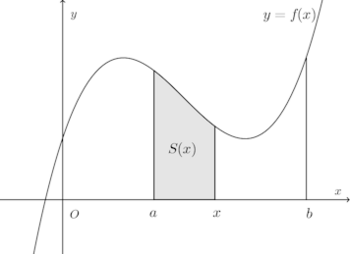

xの増分をΔxに対するS(x)の増分をΔSとすれば、

Δx>0のとき、

　　

Δx<0のとき

　　

である。閉区間[x,s+Δx]のf(x)の最大値、最小値をM、mとする。

Δx>0のとき

　　

Δx<0のとき

　　

であるから、Δxの正負にかかわらず

　　

である。

f(x)は連続だから、Δx→0のとき、m→f(x)、M→f(x)。

したがって、

　　

よって、S(x)はf(x)の不定積分の一つである。

f(x)の不定積分の一つをF(x)とすると、

　　

S(a)=0だから

　　

したがって、

　　

である。

[a,b]で囲まれた面積SはS(b)に等しい。

　　

これを関数f(x)のaからbまでの定積分といい、

　　

であらわし、a、bをそれぞれこの積分の下端、上端という。

問　次のことを証明せよ。

（１）　f(x)が偶関数ならば

　　

（２）　f(x)が奇関数ならば

　　

【解】

（１）　f(x)が偶関数ならば、f(−x)=f(x)で、y=f(x)のグラフはy軸に関して対称。

したがって、

　　

よって、

　　

（２）　f(x)が奇関数であるならば、f(−x)=−f(x)で、y=f(x)のグラフは原点に関して対称。

よって

　　

したがって、
　　

（解答終わり）

 

§２　平面図形の面積

（１）　曲線とx軸とで囲む面積

f(x)は閉区間[a,b]で連続、かつ、f(x)≧0であるとき、y=f(x)とx軸、x=a、x=bで囲まれた面積Sは

　　

である。

[a,b]でf(x)≦0のとき、曲線y=f(x)とx軸、x=a、x=bで囲まれた面積Sは、y=f(x)とx軸に関して対称なy=−f(x)とx軸、x=a、x=bで囲まれた面積に囲まれ面積に等しいから

　　

また、[a,c]でf(x)≧0、[c,b]でf(x)≦0のとき

　　

以上をまとめて

　　

である。

問　曲線y=x³−2x²−x+2とx軸とで囲まれた面積を求めよ。

【解】

　　

したがって、この曲線のグラフは次のようになる。

よって、求める面積は

　　

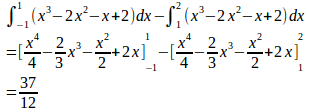
（解答終わり）

求める面積は

　　

ではなく、

　　

であることに注意！！

また、偶関数・奇関数の積分の性質を使って

　　

とすると、計算がすこし楽になる。

（２）　２つの曲線の囲む面積

２つの曲線y=f(x)、y=g(x)と直線x=a、x=bで囲まれた面積は、[a,b]でf(x)≧g(x)のとき、

　　

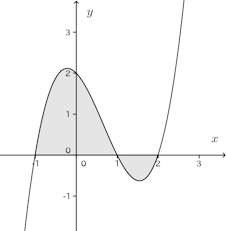
問　２つの曲線y=(x−1)³とy=x²−1によって囲まれた２つの部分の面積を求めよ。

【解】２曲線の概形は次のとおり。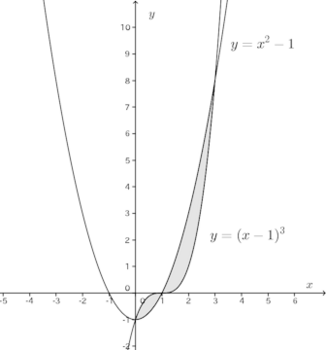



y=(x−1)³とy=x²−1との交点のx座標を求める。

　　

0≦x≦1では、y=(x−1)³≧y=x²−1
1≦x≦2では、y=x²−1≧y=(x−1)³
よって、求める面積Sは
　　

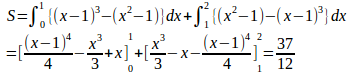
（解答終わり）

タグ：微分積分