偶関数と奇関数の積分

偶関数と奇関数の積分

偶関数とは、f(−x)=f(x)が成立する関数のことで、y軸に関して対称な関数。

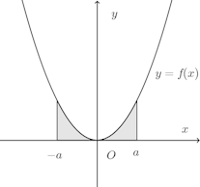
だから、

　　

が成立する。

たとえば、f(x)=x²がその代表的な例であり、

　　

になる。

対して奇関数は、f(−x)=f(x)である関数のことで、これは原点に関して対称である。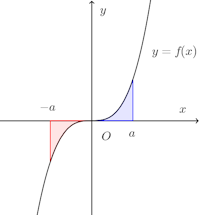

だから、

　　

である。

f(x)=x³がその代表的な例で、

　　

となる。

このことは、上の図を見れば、幾何学的に明らか。

0≦x≦aでf(x)≧0であるとき、

図の中で青で塗られている部分の面積S₁は

　　

赤の部分の面積S₂は

　　

赤で示されている領域は、青で示されている領域を原点を中心にして180°回転させたものだからS₂=S₁で、それゆえに

　　

である。

ということで、例えば、f(x)=x⁴+x³+x²+x+1の場合、

　　

g(x)=x⁴+x²+1、h(x)=x³+xとすると、g(−x)=g(x)だから偶関数、そして、h(−x)=−h(x)だから奇関数。

したがって、

　　

となるので、

　　

と、関数の偶奇性を使って、定積分の計算の省力化をはかることができる。

今やっているのは整関数だけれども、この性質は一般に成立する。

たとえば、

　　

という関数があるとする。

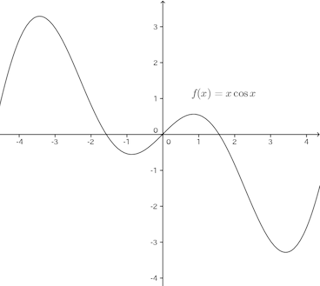
これは図から明らかなように、奇関数なので、計算をするまでもなく、

　　

であることがわかる。

（定）積分では、この性質をよく使うので、知っておくと何かと重宝する。

タグ：微分積分