高次導関数 [ネコ騙し数学]
高次導関数
関数y=f(x)の導関数f'(x)もまたxの関数であり、これをさらに微分して得られる導関数をy=f(x)の第2次導関数といい、
などの記号であらわす。
d²y/dx²は
すなわち、
同様に、第2次導関数f''(x)を微分して得られる導関数をy=f(x)の第3次導関数といい、
などであらわす。
一般に、y=f(x)をn回微分して得られる関数をy=f(x)の第n次導関数といい、
また、第2次導関数以上の導関数をf(x)の高次導関数という。
例1
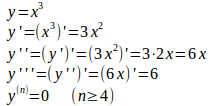
例2
問題1
とおき、両辺のr次導関数を考えることによってを定め、それから
の展開式を求めよ。
の両辺をxで微分すると、
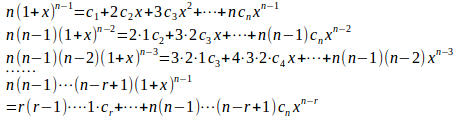
これらの両辺にx=0を代入し、係数を比較すると、
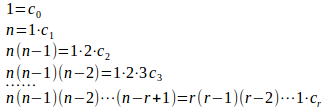
よって、
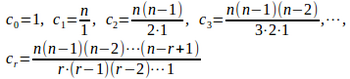
したがって、
(解答終わり)
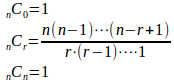
だから、この組み合わせを使うと、
x=b/aとし、両辺にをかけると
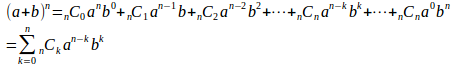
となり、2項定理が得られた。
問題2
【解】
(2) ①にx=−1を代入すると、
(3) ①の両辺を微分すると、
(4) ②にx=−1を代入すると、
問題3 f(x)がn次の整式であるとき、次の等式が成り立つことを証明せよ。
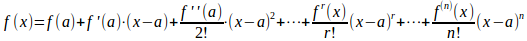
【解】
f(x)はn次の整式だから
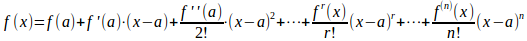
である。
(解答終わり)これは多項式、整式に対するx=aにおけるテーラー展開。
そして、このことから、f(x)をx−aで割った余りがf(a)、(x−a)²で割った余りがf(a)+f'(a)(x−a)、そして、(x−a)³で割った余りが
タグ:微分積分
2016-09-05 00:48
nice!(4)
コメント(0)
トラックバック(0)
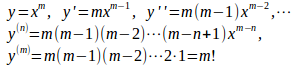




コメント 0