指数関数の微分と凹凸

指数関数の微分と凹凸

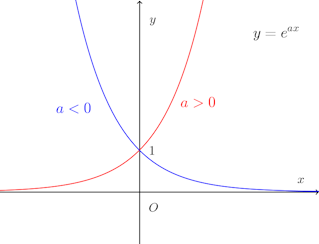
指数関数の微分は

　　

さらに

　　

では、問題を。

問題１　次の関数の凹凸を調べよ。

　　

【解】

　　

a≠0だからa²>0。よって、f''(x)>0となり、f(x)は下に凸である。

（解答終わり）

問題２　次の関数のグラフの概形をかけ。

　　

【解】

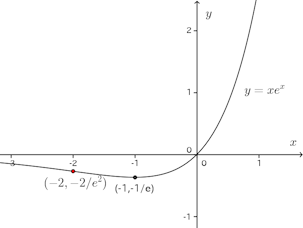
（１）

　　

とおくと、

　　

したがって、x=−1で極小で極小値は

　　

f''(x)は

　　

凹凸表を書くと

x	…	−2	…
f''(x)	−	0	＋
f(x)	上に凸	変曲点（−2/e²）	下に凸

したがって、グラフは以下の通り。

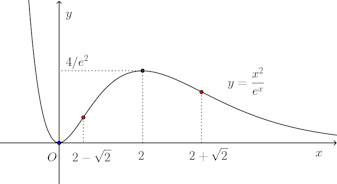
（２）

とおいて、
　　

増減表を書くと

x	…	0	…	2	…
f'(x)	−	0	＋	0	−
f(x)	減少	極小（0）	増加	極大（4/e²）	減少

２次導関数f''(x)は

　　

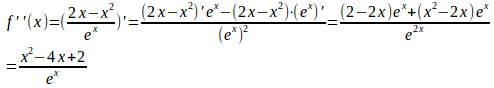
となる。

分母はつねに正なので、f''(x)の符号は分子であるx²−4x+2の符号と同じ。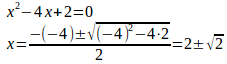
　　

したがって、凹凸表は次のようになる。

x	…	2−√2	…	2+√2	…
f''(x)	＋	0	−	0	＋
f(x)	下に凸	変曲点	上に凸	変曲点	下に凸

グラフは次の通り。

（解答終わり）

なのですが、これらのグラフを正確に書くためには

　　

が必要になる。

ということで、次の問題。

問題３　x>0のとき、次の不等式が成立することを証明せよ。

　　

【解】

n=1のとき、x>0で

　　

が成り立つことを証明する。

　　

とすると、x>0で

　　

したがって、f(x)はx>0で単調増加。

ゆえに、

　　

n=kのとき

　　

が成り立つと仮定する。

n=k+1のとき

　　

とし、xで微分すると

　　

①より

　　

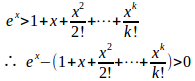
したがって、x>0でf'(x)>0となり、f(x)は単調増加。

よって、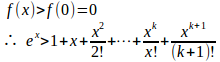
　　

となり、n=k+1のときも成立する。

以上のことより、数学的帰納法によって

　　

である。

（解答終了）

ということで、

x>1のとき、
　　

で、

　　

だから、ハサミ打ちの定理より、

　　

だから、問題２の（２）の

　　

はx→∞のとき、y→0である。

（１）の場合は、t=−xとおくと、x→−∞のときy→+∞になることを利用して

　　

このことから、x→−∞のときy→0になることが分かる。

さらに、t=logxとおくと

　　

さらに、x→∞のとき、t→+∞になることを利用して

　　

前回の極限を求めることができた。

タグ：微分積分