y²=f(x)のグラフの概形をかく [ネコ騙し数学]
y²=f(x)のグラフの概形をかく
陰関数の定義
x、yの関係式f(x,y)=0に対して、関数y=φ(x)が
を満たすとき、y=φ(x)をf(x,y)=0によって定まる陰関数という。
とって付けたように、陰関数の定義をあらたに与えたところで、さっそく、問題。
問題1 方程式y²=x⁴−2x²によって表される曲線のグラフをかけ。
【解】
また、
yは実数だからy²≧0。よって、
この関数は偶関数だから、x≧0について考えればよい。(x<0のグラフの部分はx>0のグラフをx軸で折り返せばよい)
つまり、
これを微分すると(※)
x | 0 |
| √2 | … | √3 | … |
y'' |
|
|
| − | 0 | + |
y |
|
|
| 上に凸 | 変曲点 | 下に凸 |
まず、このグラフをかき、それをy軸で折り返す。
で、
以上のことより、次の図になる。
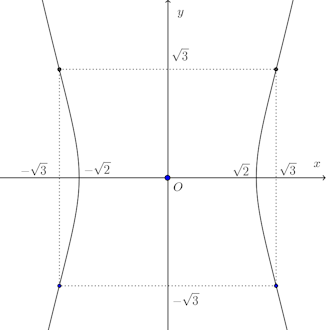
(解答終わり)
なのですが、この曲線は問題1の解答の
この組み合わせで考えると、いくらか楽になる。
なお、この曲線(?)上の点は(0,0)にも存在する。この点(0,0)のように、その近傍にそれ以外に曲線上の点が存在しない点のことを孤立点という。
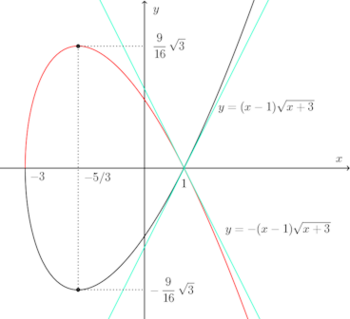
問題2 関数の増減を調べて次の方程式のあらわす曲線の概形をかけ。
(1) y²≧0だから、x≧−3。
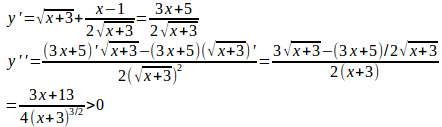
したがって、yは、x=−5/3で極小値をとり、極小値は−16√3/9。
(2)
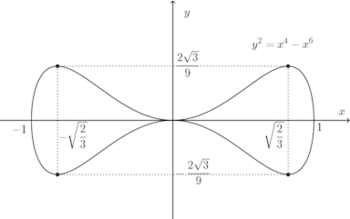
(解答終わり)
高校の微分積分の範囲内でも、これらの曲線の概形を描くことはできるけれど、これらは大学の数学の範囲でしょう。
問題3 定点(1,1)を通り、定直線x+y=0に接する円の中心P(x,y)の軌跡をCとするとき、軌跡Cの方程式を求め、そのグラフをかけ。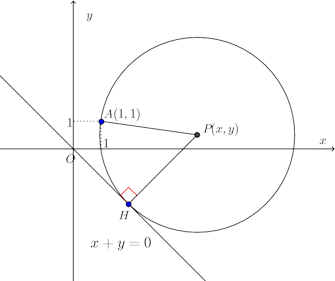
定点(1,1)をA、P(x,y)から直線x+y=0に下ろした垂線の足をHとすると、PA=PH=円の半径である。よって、
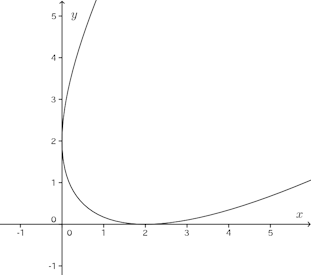
(解答終了)
この曲線の正体が何か、少しわかりづらいと思うのですが、この曲線を45°反時計回りに回転させると、次のような曲線になり、この曲線の正体が放物線であることがわかる。
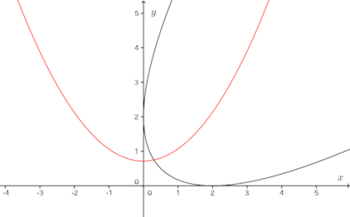




コメント 0