平均値の定理の不等式への応用

平均値の定理の不等式への応用

平均値の定理

関数f(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能ならば、

　　

であるcが少なくとも１つ存在する。

平均値の定理は、微分積分において最も重要な基礎定理。そして、応用範囲の広い定理でもある。この平均値の定理を不等式の証明に利用するというのが今回の目的である。

平均値の定理を不等式の証明に使う場合、①よりは、次のように変形したほうが使いやすい。

　　

f(b)−f(a)という関数の差の形が出たら、平均値の定理の利用を考える。

問題１　平均値の定理を利用して、x>0のとき、次の定理を証明せよ。

　　

【解】

logtは、[x+1,x]で連続、(x,x+1)で微分可能。

したがって、平均値の定理より、

　　

となるcが少なくともひとつ存在する。

x<c<x+1だから

　　

（解答終わり）

 

問題２

　　

とする。次の問いに答えよ。

（１）　0<x<aで減少関数であることを証明せよ。

（２）　0<x<aでyの値の範囲を求めよ。

【解】
（１）　yを微分すると

　　

x<c

だから

　　

x−a<0だから、y'<0

よって、yは0<x<aで減少関数である。

（２）

　　

よって、

　　

また、

　　

yは減少関数だから

　　

よって、

　　

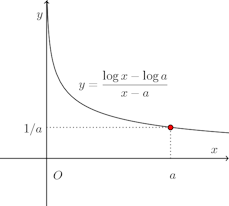
（解答終わり）

 

（２）は胡散臭くて嫌だな・・・。

問題３　すべての実数xに対して定義された関数f(x)の第２次導関数f''(x)がつねにf''(x)>0を満足するとする。このとき次の命題を証明せよ。

（１）　cを定数とするとき、すべての実数xにたいして

　　

が成立する。

（２）　任意の実数p、q、rに対して

　　

が成立する。

【解】

（１）

　　

とおく。

　　

f''(x₀)>0だから、x=cのとき、g(x)は最小で、g(c)=0。

よって、

　　

（２）

　　

とおく。

（１）より

　　

片々を足し合わせると、

　　

①より

　　

よって、②は

　　

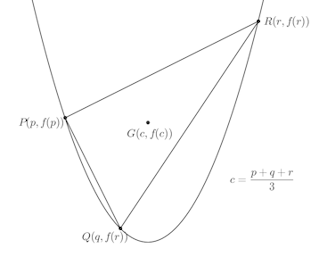
（解答終了）

タグ：微分積分