２次関数の面積の公式

２次関数の面積の公式

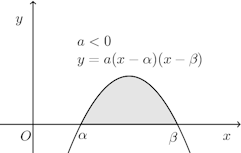
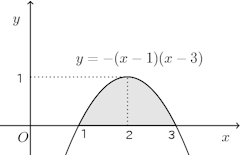問題１　放物線y=−(x−1)(x−3)とx軸で囲まれる部分の面積を求めよ。

【解】

放物線y=−(x−1)(x−3)とx軸の交点のx座標はx=1、x=3。

　　

したがって、面積Sは
　　

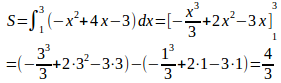
（解答終了）

すこし計算に工夫をするならば、次のように計算することもできる。

【別解】

　　

したがって、
　　

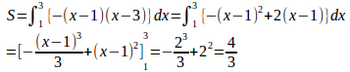
（別解終了）

大袈裟だけれど、t=x−1とおいて次のように置換積分を用いて計算することもできる。

【別解２】

x−1=tとおくと、x=t+1。

x=1はt=0、x=3はt=2に対応し、dx=dtだから
　　

（別解２終了）

なのですが、実は、次のような便利な公式が存在する。

　　

この公式を使うと、問題１の答えは、α=1、β=3とおき、

　　

と簡単に求めることができる。

公式（１）の証明は、問題１の解答のように真面目に計算すると、計算が大変なので、別解の手法を用いて証明することにする。

【公式（１）の証明】

　　

だから、
　　

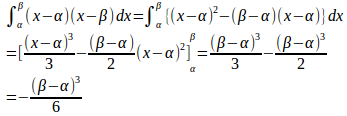
（証明終わり）

ということで、

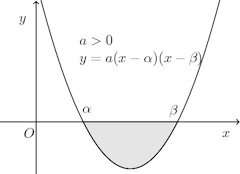二次方程式ax²+bx+c=0の解をα、βとするとき、放物線y=ax²+bx+cとx軸とで囲まれる面積Sは、

　　

二次方程式ax²+bx+c=0の解がα、βだから、

　　

になるから、公式（１）より（２）を容易に導ける。

（２）に絶対値がついているのは、α<βとすると、x軸と放物線yとの位置関係より、

a>0のとき、面積は

　　
a<0のとき

　　

になるから。

 

問題２　次の部分の面積を求めよ。

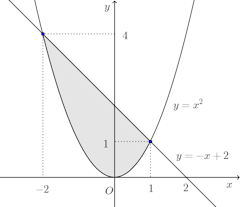
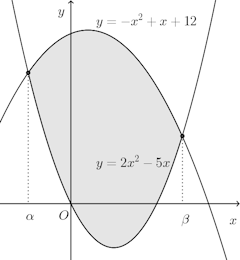
（１）　放物線y=x²と直線y=−x+2とで囲まれた部分

（２）　２つの曲線y=2x²−5x、y=−x²+x+12

【解】

（１）　放物線y=x²と直線y=−x+2との交点のx座標を求めると、

　　

よって、面積Sは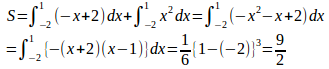
　　

（２）　２つの曲線y=2x²−5x、y=−x²+x+12の交点を求める。

　　

α=1−√5、β=1+√5とおくと
　　

β−α=2√5だから、

　　

（解答終了）

 

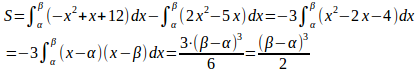
問題２の（１）は

　　

と真面目に計算してもいいけれど、それでも、やはり計算が大変だ。まして、（２）は根号を含む計算だからなおのこと大変。公式（１）の有り難みを理解できるのではないか。
（２）では、実際に、交点のx座標を求めているけれど、２次方程式①の解と係数の関係より、α+β=2、αβ=4となるので、α<βとすると、

　　

と計算することもできる。

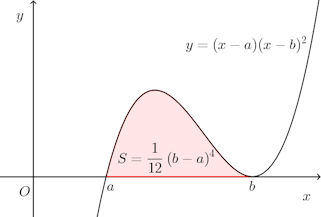
問題３　次の等式が成り立つことを証明せよ。

　　

【証明】

　　

したがって、
　　

（証明終了）

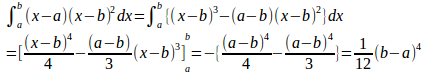
タグ：微分積分