第41回 シュワルツの不等式 [ネコ騙し数学]
第41回 シュワルツの不等式
という不等式を見たり、教科書の練習問題で証明したことはあるのではないでしょうか。
この証明は、左辺と右辺の差を取ると、つまり、左辺-右辺が
もっと一般的に
①の証明は、
λを実数とするとき、
となるので、
となる。
これは任意の実数λで成立するので、
とすると、
でなければならない。
よって、
になる。
といった感じでやればいいにゃ。
ここに出てくるDは二次方程式のところでやった判別式ですにゃ。
そこで、
すべての実数xで
が成立するとき、
という話をしましたにゃ。
とおけば、こうなることがわかりますにゃ。
他にも証明の仕方がありますけれど、これが一番わかりやすいと思いますにゃ。
ほいで、
といったデカルト直交座標の三次元ベクトルと考え、
ベクトルの内積を
という風に定義すりゃ~、
となり、
シュワルツの不等式は、
で
のとき(この仮定はゼロ割を禁止するため)、
シュワルツの不等式は
となり、
となるので、
とおけるケロ。
つまり、
となるんだケロ。
あるいは、
③を内積の出発点にして、
を導くかは流儀の違い。
高校では③でベクトルの内積を定義しているじゃないかな。
いずれにせよ、
ベクトルの内積を用いてかけば、シュワルツの不等式は、
となるけろ。
積分の場合
積分の場合は、
シュワルツの不等式は、
[a,b]でf(x)、g(x)が連続であれば
となるケロ。
証明は、λを実数とすると
だから、
となる。、
後は自分でやるケロ。
前の証明の記号をこう置き換えるだけだにゃ。
って、ことはだよ。
で、
連続関数の内積を定義できると思わないケロか。
内積やベクトルを幾何の範疇にとどめておくことはないと思わないケロか。
代数、幾何(ベクトル)、微分積分(解析)と分けて考えることがナンセンスじゃないんだろうか?
もっと自由に考えていいんじゃなかろうか?
実は、有界閉区間の連続関数はベクトルと考えても何の問題もない。
―――ベクトルの公理をすべて満たしている!!―――
そして、・・・。
内緒だケロ(笑)。
これは、微分積分の範囲を超えてしまうにゃ。
これは何を意味しているんだろうか?
これらの関数は、互いに直交しているのではなかろうか?
シュワルツの不等式は役に立つのか?
数学の基礎理論や、落とすための試験である大学入試以外じゃ、ほとんど使わない不等式だわな~。
実生活においても、まったく役に立たない不等式と言っていいんじゃないか。
でも、難関大学の数学の問題には、結構、よく出るみたいですな~。
問題を作りやすいから(ポリポリ)。
ネムネコも問題を作ってみるにゃ。
問題2 0 ≦ x ≦1で連続、かつ、f(x) > 0ならば
を証明するケロ。
問題1は、
シュワルツの不等式を使うと、
と出てくるケロ。
問題2は、
として積分のシュワルツの不等式に代入すれば、
で、この両辺の対数を取れば、
が出てくる(ポリポリ)。
積分区間の限界を変えて、
とすれば、
受験生は試験会場で悲鳴を上げるに違いない(ポリポリ)。
悲嘆にくれ、涙するんじゃなかろうか。
見た目のおどろおどろしさに騙されちゃ~、いけない!!
ちなみに、
ベクトルの内積を用いた余弦定理の証明は、
とかやります。
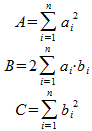
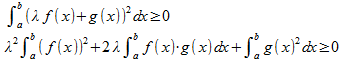
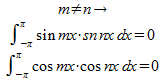
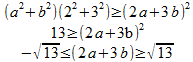
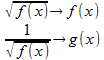
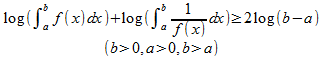
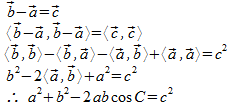




コメント 0