第４３回 三角関数の逆関数 [ネコ騙し数学]
第４３回 三角関数の逆関数
これまで何度も三角関数の逆関数を使っておきながら、これまで、三角関数の逆関数について何も触れてこなかったにゃ。
これは良くないにゃ。
ということで、急遽、三角関数の逆関数についてやりますにゃ。
三角関数のおさらい
ねこ騙し数学の公式集に書きましたけれども、
三角関数のcosθ、sinθは、
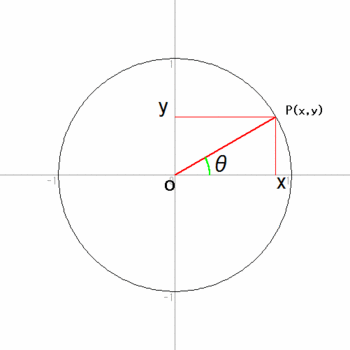
半径１の単位円周上の点Ｐと原点Ｏがｘ軸となす角度（反時計回りが正）がθのときの、Ｐのｘ座標、ｙ座標で定義されますにゃ。
つまり、
cosθ = x
sinθ = y
にゃ。
単位円と三角関数の図を見るとわかるけど、
0 ≦ θ ≦ 90° (π/2 rad) のとき 0 ≦ sinθ ≦ 1, 0 ≦ cosθ ≦ 1
–90° (－π/2 rad) ≦ θ ≦ 0のとき－1 ≦ sinθ ≦ 0, 0 ≦ cosθ ≦ 1
となるケロ。
この図は、そういう風に見るんだにゃ。
知っていると思うけれど、正弦関数と余弦関数のグラフは次のようになるにゃ。
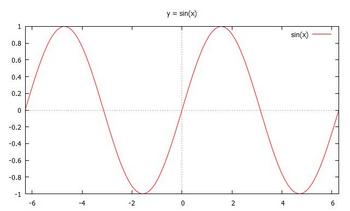
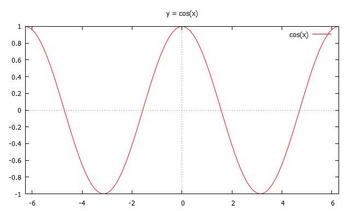
この二つのグラフを見ると、y = cosxのグラフは、y = sinxのグラフを左に90°（π/2 rad）移動させたものだとわかると思うにゃ。
つまり、
y = cosxのグラフを見ればわかるけれど、cosxはｙ軸（x = 0）に対して対称だから、偶関数なので、cos(–x) = cosxということもわかるケロ。
この結果を①に使うと、
ほいで、②をじっと見ていると、t = π/2 – x と何気に起きたい気分になったので、
となり、これを②に放り込むと、
になるケロ。ここで、さり気なくｔをｘに戻すと、
が出たにゃ。
つまり、
この結果は、頭を横にして単位円と三角関数のグラフを見るとわかりますよ。
π/2 – xはｙ軸とＯＰがなす角なんで。
なお、このとき、
にすり替わっている点だけは注意してください。
さらに念押し。
正弦関数と余弦関数のグラフの横軸のｘは、角度θをｘにしたもので、単位円と三角関数のｘではないですからね。
正弦関数のときは、θ →x、x → yに、
余弦関数のときは、θ→xに変わっているので、この点は注意してくださいにゃ。
三角関数の逆関数
x∈X、y∈Ｙで、ＸからＹへの関数ｆが１対１の対応のとき逆関数が定義され、
になる。
そして、今回は使わないけれど、
という関係がある。
さてさて、三角関数を見るとわかりますが、この関数の定義域を実数全域とすると、y = sinx、y = cosxともに、１対１対応ではないので、このままでは、逆関数を定義できない。
たとえば、上の図で示したy = sinx のグラフでは、 y = 0 になる点が５つもある。
だから、１対１対応にするために、定義域を制限しなければならない。
そこで、正弦関数、sinxの場合は、-π/2 ≦ x ≦ π/2とすると、-1≦ sinx ≦ 1の単調増加関数になるので１対１対応になる。
で、-1 ≦ y ≦ 1に対して
と定義できる。
だから、
なんてことは、絶対に、ない。
かならず、
です。
で、ここで厄介なことが起きる（笑）。
－π/2 ≦ x ≦ π/2のとき、 y = cosxは、１対１対応になっていない。
だ・か・ら、
y = cosxの逆関数を定義するために、ｘの定義域を、たとえば、 0 ≦ x ≦ πに取らないといけない。
逆関数を定義するために、y = sinxとy = cosxの定義域を変えないといけない。
だから、
となります。
こっちの場合は、
は存在するけれど、
という値はありません。
で、これらのグラフは以下のとおりです。
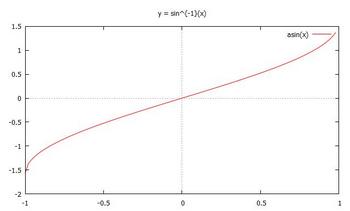
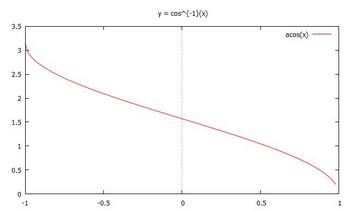
コンピュータは、
や
を計算できないようなので x = 1のところで切れていますが。
なお、この図は、頭を横にすると、x = siny、 x = cosyの一部になっていることがわかりますにゃ。
ところでところで、実は、この逆関数の定義域の違いの問題が、逆関数の微分の符号に関係していますにゃ。
逆関数の微分は
だったにゃ。
だから、
となるケロ。
だけれども、
の定義域－π/2 ≦ x ≦ π/2 では、cosx ≧ 0 だから、⑤式の符号が取れて、
となる。
の定義域を、 π/2 ≦ x ≦ 3π/2とすると、cosx ≦ 0 なので、⑥は符号が変わる。
これは、cosxの逆関数でも同じ事情を抱えていて、
となり、sin(x)の符号の問題になるにゃ。0 ≦ x ≦ πでsinx ≧ 0 だから、
なるんだにゃ。
⑥と⑦の符号はかなり微妙で、
逆関数の定義域の取り方によって逆転するということだケロ。
タグ：微分積分
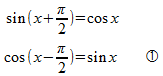
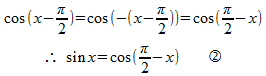
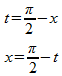
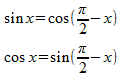
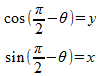
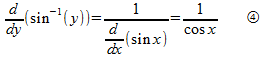
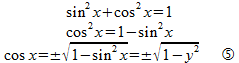
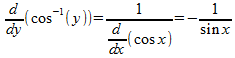
コメント 0