隣接３項の漸化式 [ネコ騙し数学]
ねこ騙し数学 隣接３項の漸化式
隣接する参考の漸化式の一般項を求める方法についての話をしますにゃ。
例題 数列
が次の関係で与えられるとき、をｎの式で表わすケロ。
【解】
だから、
となり、数列
は、初項
で公比2 の等比数列になるケロ。
よって、
また、①より
よって、
②式を③式で引くと
こんなふうに解きますにゃ。
あるいは、②式の結果を使って
これらをすべて足すと、
と求めることも出来るにゃ。
ここでは、等比級数の和の公式
を使っているにゃ。 a = 2 ,r = 2, m = n – 1 とすると、こうなることがわかるケロ。
ちなみに、
で与えられる、数列
を階差数列というにゃ。
で、k = 1, 2, ・・・, n の階差数列の和は
で、例題を一般的に書くと、
のとき、この漸化式は
になるので、
上の式を下の式で引くと
β – α ≠ 0 ならば、両辺をβ – αで割って、
で、α = β のときは、
になるので、
となり、この両辺を
で割ると、
だから、
は等差数列となり、
になるんだケロ。
じゃあ、どうやって、このαとβを求めればいいかというと、
を
として、この２次方程式を解けばいいんだけろ。
たとえば、例題は
なので、
という二次方程式にして、
になる。ちゃんと、なっているだろ？
じゃあ、この問題を解いてくんな。
問題１
【答】
であるとすれば、この数列の極限
になるわな～。
フィボナッチ数列
問題２
（１）数列 1, 2, 3, 5, 8, 13, 21, 34, ・・・ はどんな規則でできているか。その規則を式で表わせ。
（２）上の数列の第n項を第n+1 項で割ったものを
とおくとき、
を求めよ。
【答】
（１） 3 = 2 + 1
5 = 3 + 2
8 = 5 + 3
という関係があるので、
つまり、これはフィボナッチ数列！！
（２）
これをジッと見る。
で、ネムネコ、閃く！！
なので、
この両辺を
で割ると
で、
だから、
そして、
として、上の式からαを引くと
だから
α > 0だから0 < 1/(1+α) < 1となり、
n → ∞のとき
よって、
この値は何かというと、黄金比！！
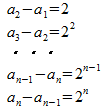
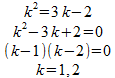
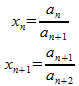
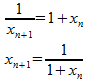
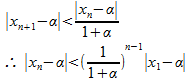
コメント 0