第３１回 関数項級数

第３１回 関数項級数

関数項級数とは
区間Iで定義された関数からなる関数列対して部分和

からなる部分和が収束するとき、関数項級数

は収束するといい、関数列の極限関数S(x)であるとき、関数項級数の和はS(x)であるという。

このことを

と表す。

解析的には任意のε > 0 に対し

となるNが存在する。

これまでに何度か出てきたコーシーの判定条件をつかって言い換えるならば、次のような定理になるケロ。

定理
間Iで定義された関数を項とする関数項級数が収束するためには、任意のε > 0 に対して
となるような正の整数Nが存在することが必要十分である。

関数項級数といっても、これは関数列の一種なので、これまでにやってきた関数列だからね。なので、各点収束や一様収束を定義することができるケロ。

関数項級数は、その部分和からなる関数列が一様収束するならば、一様収束だにゃ。が各点収束するならば、各点収束だにゃ。

例 I = [-1,1]のとき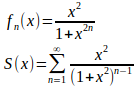

とすると、これはx = 0 では S(x) = 0 、それ以外では

になる。何故ならば、

で、S(x)の部分和は初項、公比等比数列の和となり、その極限は


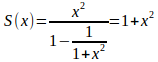
となるから。

よって、

となり、この（極限）関数は x = 0 で不連続になるにゃ。

そして、このことから、この関数項級数は一様収束ではなく、各点収束であることがわかるケロ。

一様収束する例は無数にあるのだけれど、これをいうためにはさらにいろいろなことをやってからでないとちょっと難しいので、今回は関数項級数のさわりということで。

---

今回は諸般の理由から、
いつもと違うソフトからこのねこだまし数学ん下書き原稿を作りましたので、見苦しいと思いますが、
今日のところは勘弁してください。
改めて後日、この記事はアップしたいと思います。

タグ：級数 数列 極限 関数列