第１７回 積分記号のもとでの微分

第１７回　積分記号のもとでの微分

「積分記号のもとでの微分」とは何かというと、K=[a,b]×[α,β]で定義された関数f(x,t)で

　　

が成り立つかどうかというもの。

試しに、f(x,t)=xyという関数でやってみると、

左辺は

　　

となり、右辺は

　　

となり、K上でf(x,t)が連続、かつ、偏導関数が連続の条件があれば、成り立つのであろうと予想できる。
f(x,y)が偏微分可能でなければ、そもそも右辺のは存在しないし、これがK上で連続でなければ右辺の積分が存在する保証がないので。

ということで、この予想が正しいかどうかをこれからやるにゃ。
すぐには出来ないので、まず、次の定理。

定理17-1

関数f(x,t)がK=[a,b]×[α,β]で連続であるとする。このとき、

　　
は連続である。

【証明】

f(x,t)は有界閉区間K上での連続関数だから一様連続。よって、任意の正数εに対して

　　

となるδが存在する。

故に、ならば

　　

となり、連続である。

（証明終わり）

そして、今回のメインである次の定理。

定理17-2（積分記号のもとでの微分）

f(x,t)は有界閉区間K=[a,b]×[α,β]上の連続関数で、偏導関数も連続であるとき、関数は[α,β]上で微分可能で

　　
である。
【証明】

f(x,t)はK上の連続関数なので重積分可能であり、累次化ができる。よって、

　　

定理17-1よりは連続であり、

　　

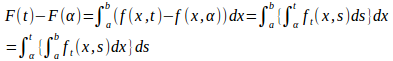
は微分可能である。

（証明終わり）

上の定理の証明の最後の部分では、g(t)が[α,β]上で連続ならば

　　

という積分の定理を使っているにゃ。

ということで、f(x,t)が有界閉区間K上の連続関数で、さらに偏導関数がK上で連続であれば、①が成り立つことがわかった。

問題１　次の値を求めよ。ただしa>0とする。

　　

【解】

　　

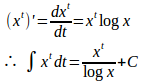
だから、

　　

となる。
また、は[0,1]×[0,a]で連続だから、

　　
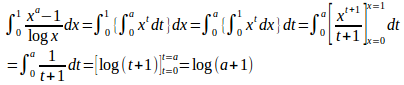
（解答終わり）

ちょっと難しくて、計算が面倒くさい問題を一つ上げるにゃ。

問題２　について、次のことが成り立つことを示せ。

　　

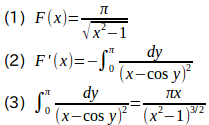
【解】

（１）を求めるには、とおいて置換積分を使うのだけれど、この計算は結構大変だし、今回の内容と直接関係しないから、やらないにゃ(^^ゞ
（２）は

（３）は（１）を微分すれば、

　　

になるので、・・・。
（解答終わり）

そして、（３）をさらにｘで微分すると、

　　
さらに、微分を繰り返して

　　
と、微分を繰り返すことで積分の値をどんどん求めることができるんだにゃ。

タグ：重積分