定積分と面積の問題１

定積分と面積の問題１

問題１　曲線y=x³−4xと、その上の１点(1,−3)における接線とが囲む図形の面積を求めよ。

【解】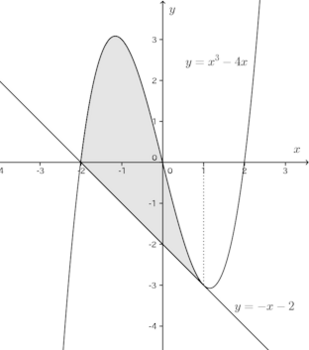

y'=3x²−4だから、点(1,−3)における接線の方程式は

　　

y=x³−4xとy=−x−2との交点を求める。

　　

よって、求める面積は

　　

（解答終わり）

 

問題２　３次関数f(x)がある。f(x)はx=−1およびx=2で極大または極小となり、曲線y=f(x)上の点(0,1)における接線の方程式は3x−2y+2=0である。この曲線と接線で囲まれる図形の面積を求めよ。

【解】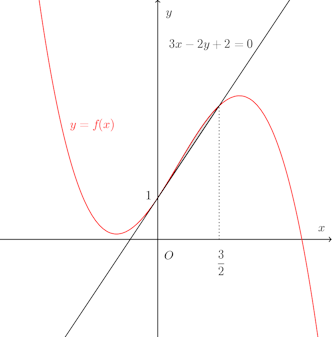

３次関数f(x)はx=−1とx=2で極値を取るので

　　

よって、

　　

この曲線は点(0,1)を通るので

　　

また、点(0,1)における接線は3x−2y+2=0で、接線の傾きが3/2だから

　　

y=f(x)と3x−2y+2=0の交点のx座標はx=0,3/2だから

　　

（解答終わり）

 

問題３　放物線y=x²+x+1と、原点からこの放物線に引いた２本の接線とで囲まれる部分の面積を求めよ。

【解】

原点から放物線に引いて接点を(a,a²+a+1)とすると、接線の方程式は

　　

原点を通るので

　　

よって、接線の方程式は、y=2x、y=−x。

したがって、求める面積Sは

　　

（解答終わり）

 

問題４　（１）　y=x³に３本の接線が引けるP(a,b)の存在する範囲を図示せよ。

（２）　（１）で求めた範囲でx²+y²≦2を満たす部分の面積を求めよ。

【解】

（１）　接点を(t,t³)とすると、接線の方程式は

　　

点P(a,b)を通るので

　　

f(t)=2t³−3at²+bとおくと

　　

よって、f(t)はt=0、t=aで極値をもつ。

f(t)=0が３つの実根をもつ条件は極大値×極小値<0だから

　　

P(a,b)の存在領域は次のとおり。


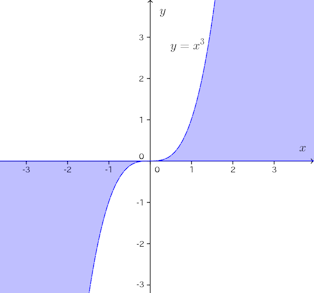
（y=x³とx軸は含まない）。

（２）　求める面積は、図に示す扇型OABの面積から灰色の面積を引いたものを２倍したもの。

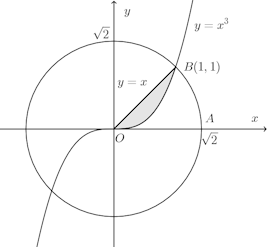
灰色の部分の面積は

　　

扇型OABの面積はπ/4だから、

求める面積は
　　

タグ：微分積分