３次方程式２

３次方程式２

問題１　３次方程式x³+px+q=0が重複解をもつとき、

　　

なる関係があることを証明せよ。

【解】

f(x)=x³+px+qとおき、３次方程式f(x)=x³+px+q=0の重複解をαとすると、

　　

であり、

　　

f(x)を微分すると

　　

したがって、

　　

③より

　　

①より

　　

④と⑤より

　　

（解答終わり）

②の微分のところでは、次の微分公式を使っている。

　　

問題２　３次方程式x³+px²+q=0が重複解をもつとき、pとqにはどのような関係があるか。

【解】

f(x)=x³+px²+qとおき、αを重複解とすると、

　　

よって、

　　

②より
　　

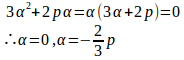
（１）　α=0のとき、①よりq=0。

（２）　のとき、これを①に代入すると

　　

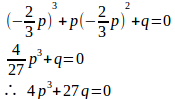
よって、

4p³+27q=0、または、q=0。

（解答終わり）

ちなみに、p=q=0のときは、３重解でx=0が解。

問題３　a、b、cが相異なる実数で、

　　

のとき、ab+bc+caの取りうる範囲を求めよ。

一見すると、３次方程式とは関係なさそうな問題ですが・・・。

【解】

　　

とすると、

　　

これが成立するのは、次の３次方程式

　　

が相異なる３つの実数解をもつということ。

３次方程式の解と係数の関係より、

　　

①はx=0を解に持たないので、

　　

①は②と同値。

　　

とおくと、

　　

よって、f(t)はで極小値をとる。

　　

f(x)のグラフは次のようになる。

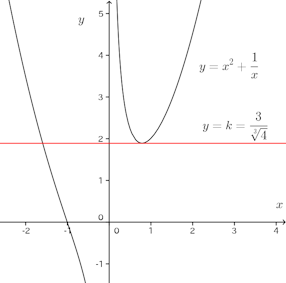
f(x)=kの実数解の個数とy=kとy=f(x)の交点の個数は等しいので、相異なる③つの実数解をもつためには

　　

したがって、

　　

（解答終わり）

次のように、y=x³+1とy=kxとの交点の数を調べて、kの範囲を定めてもよい。。

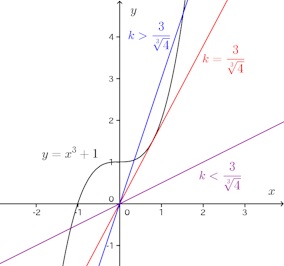
曲線y=x³+1上の点(t,t³+1)における接線の方程式は

　　

これが原点を通るとすると
　　

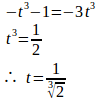
この時の傾きは

　　

したがって、y=kxがy=x³+1とに接するとき

　　

よって、y=kxとy=x³+1の交点の数、つまり、x³−kx+1=0の実数解の個数が３のとき、