2次導関数を用いた極値の判定

2次導関数を用いた極値の判定

定理　関数f(x)が連続な導関数f'(x)、f''(x)を有する区間内において、

　（Ⅰ）　f'(a)=0、f''(a)>0のときはx=aでf(x)は極小

　（Ⅱ）　f'(a)=0、f''(a)<0のときはx=aでf(x)は極大

【証明】

（Ⅰ）　f''(x)は連続でf''(a)>0だから、aを含む小さな開区間Iに属するxでf''(x)>0。したがって、f'(x)は開区間Iで増加状態にある。さらに、f'(a)=0だから、aの前後でf'(x)の符号が負から正に変わる。よって、x=aで極小である（※）。

（Ⅱ）　aを含む小さな開区間Iに属するxでf''(x)<0。したがって、f'(x)は開区間Iで増加状態にある。さらに、f'(a)=0だから、aの前後でf'(x)の符号が正から負に変わる。よって、x=aで極大である。

（証明おわり）

（※）　f'(x)の符号がx=aの前後で負から正に変わるとき、f(a)は極小である。

x<aのとき、平均値の定理より

　　

となるcが存在し、f'(c)<0、x−a<0だから、

　　

a<xのとき

　　

となるcが存在し、f'(c)>0、x−a>0だから

　　

同様に、f'(x)の符号が正から負に変わるとき、x=aで極大であることが証明される。

ここで平均値の定理を使うならば、

　　

を使えという指摘もあるだろう。

もっともな話である。

これを使うならば、f'(a)=0だから

　　

|h|が十分小さくとれば（h≠0）、f''(a+θh)とf''(a)の符号は同じ。

よって、f''(a)>0ならば

　　

したがって、x=aで極小。

f''(a)<0ならば

　　

したがって、x=aで極大。

スッキリとした証明になるが、さすがに、この証明は高校数学の範囲外だろう。

⑨は、まだ証明していないし・・・。
ただし、これは２次導関数が連続であればの議論！！

定理　f(x)が[a,b]において連続、f(x)が(a,b)において２回微分可能であるとき、

　　

となるcがaとbの間にすくなくとも一つ存在する。

【証明】

　　

が成り立つようにkを定め、

　　

とすると、F(x)は[a,b]で連続、(a,b)で微分可能である。

　　

F(a)=F(b)=0だから、ロールの定理より、F'(c)=0、すなわち、

　　

となるcがaとbの間に少なくともひとつ存在する。

b≠cだからb−c≠0。

②の両辺をb−cで割ると

　　

これを①に代入すると、

　　

（証明終わり）

 

問　f(x)=x³−3x−1の極値を求めよ。

【解】

　　

よって、f'(x)=0を満たす点はx=±1。

　　

したがって、x=−1のとき極大、x=1のとき極小。

　　

極大値　1　(x=−1のとき)

極小値　−3　（x=1のとき）

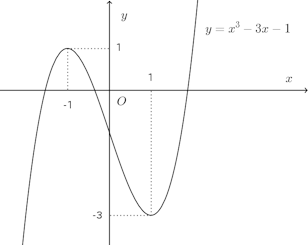
（解答終わり）

 

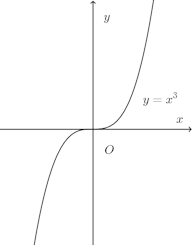
しかし、この判定法もf(x)=x³の前には無力！！

f'(x)=3x²、f''(x)=6xだから、x=0のときf''(0)=0となって、第２次導関数を利用した判定法が使えない。

この関数はかなりの曲者！！

タグ：微分積分