曲線の凹凸

曲線の凹凸

§１　曲線の凸凹

xのある区間で連続な曲線y=f(x)を考える。この区間内にある任意の２点P、Qに対してP、Qを結ぶ曲線の弧がつねに線分PQの下にあるとき、曲線y=f(x)はこの区間で下に凸（または上に凹）であるという。反対に、弧PQがつねに線分PQより上にあるとき、曲線y=f(x)はこの区間で上に凸（または下に凹）という。

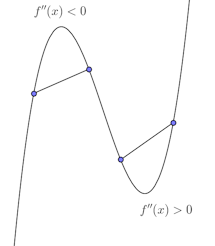
曲線の凸凹は、第２次導関数f''(x)の符号で判定できる。

（１）　f''(x)>0である区間で曲線y=f(x)は下に凸である

（２）　f''(x)<0である区間で曲線y=f(x)は上に凸である

 

（１）の証明は次のとおり。

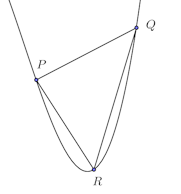
この区間にある曲線y=f(x)上に２点P、Q

　　

をとり、曲線PQ上の任意の１点をR(x,y)とすると、平均値の定理より

　　

となるc、dが存在する。

f''(x)>0であるから、f'(x)は単調増加であり、したがって

　　

よって、①、②より

　　

x−x₁>0、x₂−x>0だから

　　

x₂−x₁>0だから

　　

③は、R(x,y)が直線PQ

　　

より下にあることを示しており、すなわち、曲線の弧PQが線分PQより下にあり、したがって、この曲線はこの区間において下に凸である。

同様に、（２）も証明される。

問題１　曲線y=f(x)について、次のことを証明せよ。

（１）　曲線y=f(x)が下に凸の区間では、曲線はつねに接線の上側にある。

（２）　曲線y=f(x)が上に凸の区間では、曲線はつねに接線の下側にある。

【解】

（１）　曲線y=f(x)が下に凸である区間の、この曲線上にある任意の点Pの座標を(a,f(a))とすると、Pにおける接線の方程式は

　　

点Pとは異なる、この区間の任意の曲線上の点Qを(x,f(x))とし、f(x)と①の差をとると

　　

平均値の定理より

　　

となるcが、a<c<xまたはx<c<aに存在する。

よって、

　　

f''(x)>0だから、f'(x)は単調増加。

したがって、

a<c<xのとき、f'(a)<f'(c)だからf'(c)−f'(a)>0、x−a>0、

x<c<aのとき、f'(c)>f'(a)だからf'(c)−f'(a)<0、x−a<0

よって、

　　

であり、曲線は接線の上側にある。

（２）も同様に証明される。

（解答終わり）

問題１より、次のことが言える。

（１）　曲線y=f(x)が下に凸の区間では、曲線はつねに接線の上側にある。

（２）　曲線y=f(x)が上に凸の区間では、曲線はつねに接線の下側にある。

 

§２　変曲点

曲線の凸凹の境目の点を曲線の変曲点という。

点P(a,f(a))が曲線y=f(x)の変曲点ならば、x=aの前後でf''(x)の符号が変わるから、f''(x)がx=aで連続ならばf''(a)=0である。

たとえば、y=x³はy''=6xだから、x<0で上に凸、x>0で下に凸で、その境目である原点がy=x³の変曲点である。

問　次の関数の凸凹を調べ、変曲点を求めよ。

（１）　y=x³−3x²+3　　　（２）　y=x³(x−4)

【解】

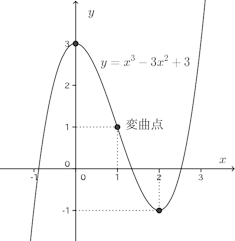
（１）

　　

したがって、x<1で上に凸、x>1で下に凸。

y=f(x)=x³−3x²+3とすると、

　　

よって、変曲点は(1,1)。

（２）
　　

したがって、x<0ではy''>0、0<x<2でy''<0、x>2でy''>0となり、

x<2で下に凸、0<x<2で上に凸、x>2で下に凸。

変曲点は、(0,0)、(0,−16)

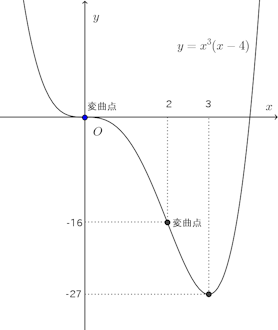
（解答終わり）

 

問題では問われていないけれど、（１）の極値はy'=3x²−6x=0を解くとx=0、2。y''=f''(x)=6(x−1)であり、これを用いて、f''(0)=−6<0だから極大、f''(2)=6>0だから極小と判定できる。
（２）は、y'=4x³−12x²=0からx=0、x=3。y''=f''(x)=12x(x−2)だから、x=0のときf''(0)=0となり２次導関数の符号を用いた判定ができない。x=3では、y''>0となり極小と判定できる。