台形公式と中点公式とによる定積分の近似計算

台形公式と中点公式とによる定積分の近似計算

定積分

　　

の近似計算法として台形公式とシンプソンの公式を紹介した。

その最も基礎となるのが、

　　

という２つの式。

（１）が台形公式で、（２）がシンプソンの公式。

（１）と（２）が幾何的に何をあらわしているか明らかにするために、

a≦x≦bにおいてy=f(x)>0という曲線を考える。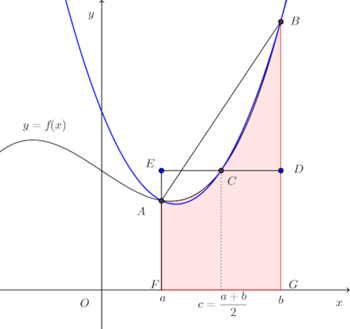

そして、A(a,f(a))、B(b,f(b))、F(a,0)、G(b,0)とする。

そうすると、

　　

は、y=f(x)とx軸、さらにx=a、x=bとで囲まれた面積に等しい。

（１）は台形ABGFの面積に等しい。何故ならば、

　　

となるからだ。

さらに、線分FGの中点のx座標をcとすると、

　　

になる。

そして、

　　

とし、A、B、Cの３点を通る放物線をg(x)（図中の青い曲線）とすると、

　　

になる。

つまり、（２）は曲線y=f(x)を放物線で近似し、その面積を求めて①で定まる面積Sを近似している。

台形公式はy=f(x)を直線で近似、シンプソンの公式では放物線で近似しているのだから、一般論として、（１）より（２）の方がより真実の面積Sに近い値を示す。

これはあくまで一般論だケロよ。

では、ここで質問する。

点a、点bの中点cにおけるf(c)を高さとする四角形DEFGの面積、すなわち、

　　

と、台形公式(1)、シンプソンの公式、そして、あらたに登場した（３）の中点公式、どちらが精度よくSを計算できるだろうか？

あくまで一般論として、中点公式（３）がシンプソンの公式に勝つことはないだろう。

だとすれば、

中点公式と台形公式の勝負だケロ。

簡単なf(x)=x²

　　

で試してみると、台形公式だと

　　

中点公式だと

　　

だから、

　　

つまり、台形公式（１）よりも中点公式(2)の方が精度よく計算できている。
上の例だと、台形公式は中点公式よりも誤差が２倍も大きい。裏を返せば、中点公式は台形公式よりも２倍精度がよい。

　　

台形公式だと変わらずS₁=1/2。

中点公式だと

　　

したがって、

　　

が成立している。

この２という数字は偶然だろうか・・・。

ちなみに、シンプソンの公式はf(x)が３次関数までは正確な値を出す。
　　

シンプソンの公式で計算してみると、

　　

２次関数で近似しているのに、３次関数まで正確な値を出す。

不思議だと思わないかい。

閉区間[a,b]をn個の区間に分割し、この区間に対して台形公式と中点公式を適用し定積分を近似すると、

　　

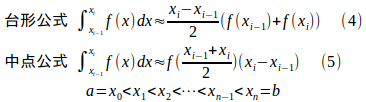
等間隔に分割されている場合、

　　

だから、

　　

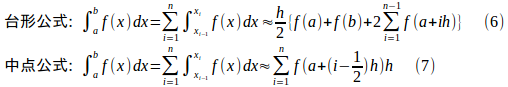
台形公式と中点公式で定積分の近似計算をするプログラムをBloggerの方にアップしておいた。

　　中点公式と台形公式の精度比較
　　　http://nemneko.blogspot.jp/2016/11/blog-post_14.html

プログラムのデフォルト設定は

　　

[0,1]の分割数nを増やすとどうなるか、この計算の場合、どちらのほうが精度がいいのかを確かめて欲しい。

ちなみに、n=10のときの計算結果は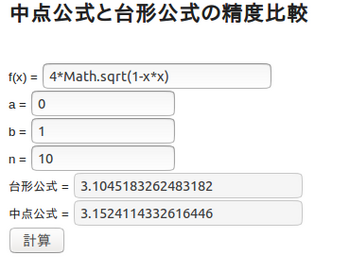

（イメージです。だから、計算ボタンをクリックしても何も起きない）

n=100のときの計算結果は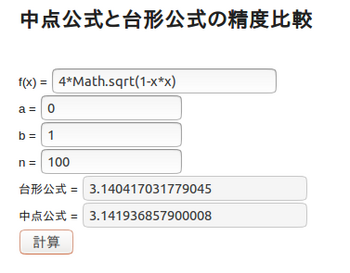

（イメージです！！）

台形公式よりも中点公式のほうが精度よく計算できていることが分かるのではないか。

タグ：微分積分