台形公式の精度を求める問題 [ネコ騙し数学]
台形公式の精度を求める問題
台形公式の精度を求めるいい問題があったので紹介します。
問題
a<bのとき
この関数について、ロールの定理を繰り返して使うことによって
【解】
x=aのとき、
x=bのとき
よって、ロールの定理よりF'(c)=0となるa<c<bが存在する。
②を微分すると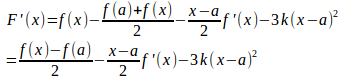
よって、F'(a)=0。
F'(a)=F'(c)=0かつ、F(x)は[a,c]で連続、(a,b)で微分可能。よって、ロールの定理より
ξ<>aだから、
(解答終了)
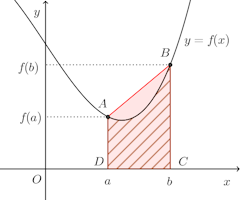
は、右図の台形ABCDの面積である。
問題の結果より、
[a,b]を
n等分したのだから、
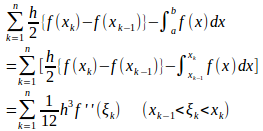
よって、
ここで、の最大値をMとすると、
ちなみに、以前紹介した中点公式
の誤差限界は
(1)と(2)のMは等しくないので単純な比較はできないけれど、Mが同一であれば、中点公式は台形公式の誤差の1/2ということになる。
だから、一般論になるけれど、中点公式の方が台形公式より精度はよいということになる。
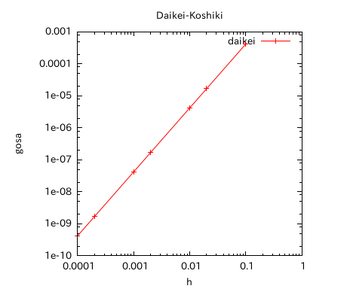
このグラフだと少しわかりにくいと思うのだが、h=0.1からh=0.01へとhが1/10になると、誤差は約その2乗である(1/10)²=1/100になる。
計算した生のデータのほうがわかりやすいと思うので、生データを以下に示す。
分割幅 h 誤差
0.010000 0.000004166667
0.001000 0.000000041667
0.000100 0.000000000417
この関数の場合、綺麗に1/100になっている。
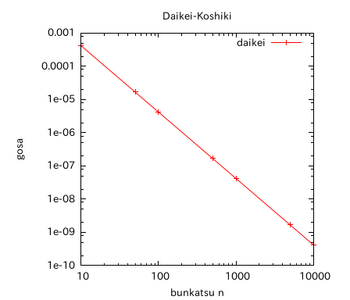 これだとまだ直観的に理解しづらいかもしれないので、[0,1]の分割数nと誤差との関係についてのグラフを示す。
これだとまだ直観的に理解しづらいかもしれないので、[0,1]の分割数nと誤差との関係についてのグラフを示す。
タグ:微分積分
2016-11-28 12:05
nice!(0)
コメント(0)
トラックバック(0)




コメント 0