ベクトル関数の偏微分

ベクトル関数の偏微分

 

ベクトルAが２つのスカラーの関数、すなわち、A=A(u,v)であるとする。

２変数のベクトル関数A(u,v)の偏導関数を

　　

で定義する。

A(u,v)のx成分、y成分、z成分をとすると、

　　

である。

 

問　ベクトル関数の偏導関数を求めよ。

【解】

Aのx成分、y成分、z成分をとすると、

　　

だから、

　　

したがって、

　　

（解答終）

 

なんとも見づらいので、ベクトル表示で次のようにしたほうがいいのだろう。

　　

 

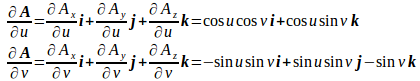
u、vの微小変化Δu、Δvに対して

　　

になるとすれば、Δu、Δvをdu、dvであらわし、

　　

をAの全微分という。

そして、uとvがtの関数、すなわち、u=u(t)、v=v(t)のとき、実関数のときと同様にチェーンルールが成立し

　　

である。

また、uとvがs、tの関数、すなわち、u=u(s,t)、v=v(s,t)のとき

　　

である。

 

曲面の方程式は、スカラー変数、u、vを用いれば、

　　

であるから、曲面上の任意の点P(x,y,z)の位置ベクトルをとすれば、曲面は

　　

で表される。これを曲面のベクトル方程式という。

vを一定としuを変化させれば、rは曲面上の曲線をあらわす。これをu曲線という。また、uを一定にしvを変化させれば、rは曲面上の曲線をあらわす。これをv曲線という。偏微分係数の定義よりあきらかなように、はu曲線の接線ベクトルであり、はv曲線の接線ベクトルである。

また、u、vが変数tの関数であるときには、は曲面上の曲線をあらわす。曲面上の点Pにおける接線ベクトルは

　　

したがって、Pを通る曲面上の曲線の接線は、が定める平面上にある。この平面を点Pにおける接平面といい、Pを通り接平面に垂直な直線を法線、Pを始点とし接平面に垂直なベクトルを法線ベクトルという。したがって、

　　

は法線ベクトルである。

 

問２　曲面z=1–x²–2y の点(1,1,−2)における接平面を求めよ。

【解】

x=u、y=vとおくと、z=1–u²–2v。よって、曲面上の点の位置ベクトルは

　　

だから、

　　

法線ベクトルnは

　　

点(1,1,−2)のときu=x=1、v=y=1だから、(1,1,−2)における法線ベクトルnは

　　

したがって、曲面z=1–x²–2y の点(1,1,−2)における接平面の方程式は

　　

（解答終了）

 

曲面z=f(x,y)上の点P(x₀,y₀,z₀)における接平面の方程式は

　　

である。

これを使うのならば、

　　

となるので、接平面の方程式は

　　

 

タグ：ベクトル 偏微分 微分