テンソルの問題とその解答(?) [ネコ騙し数学]
問題 をテンソル、
をベクトルとするとき、次が成り立つことを示せ。
(1) はスカラーである。
(2) 2次形式の値は直角座標の変換によって変わらない。
【略解】
(1) とおけば、これはベクトル。
したがって、これはスカラーである。
(2) (1)より、これはスカラー(不変量)。よって、直角座標の変換によって値は変わらない。
(略解終)
ちなみに、をベクトルとするとき、
がスカラーになることは、次のように証明すればよいだろう。
直角座標の変換によって
になるとする。
となり、直角座標の変換によって値は変わらない。
よって、
はスカラーである。
ベクトルuとvを、直交座表系O-x¹x²x³から直交座表系O-x'¹x'²x'³に
と書き換えただけで、uとvそのものが変わっているわけじゃ〜ない。
uとvの大きさ、そして、この2つのベクトルのなす角θは変わっていないのだから、どの直交座標系であろうが、
は不変!!
したがって、アタリマエのことを言っているに過ぎない。
そして、幾何的にアタリマエのこのことを、代数的に証明したということになる。
ということで、空間中にどのような直交座標系を設定し、それをもとにuとvを
と表し、これをもとに、その内積u・vを
と計算してよいということになるんだにゃ。
なお、⑨を用いてベクトルuとvの内積を計算できるのは直交座標系のとき。たとえば、x¹、x²、x³軸が互いに直交していない(斜交)座標系ではこうはならないので、この点は注意。
第8回 対称テンソル [ネコ騙し数学]
第8回 対称テンソル
をテンソル、
をベクトルとする。
対称テンソルについて
となる零ベクトルでないベクトルと数λが存在するとき、ベクトル
の方向を対称テンソル
の主方向、λをその方向の主値という。
(1)式より
となるので、
ベクトルは零ベクトルでないので、ベクトルの成分は同時に0にならない。
よって、
でならなくてはならない。
λに関する3次方程式(3)を特性方程式(固有方程式)、その解を固有値、(1)または(2)式で得られる零ベクトルでないベクトルを固有ベクトルという。
性質1 対称テンソルの固有値はすべて実数である。
【証明】
を対称テンソルとする。
特性方程式(3)の解の1つをλ、それに対応する固有ベクトルをとすれば、
λを複素数、をその共役複素数とし、(4)の両辺の共役複素数をとれば、
(4),(5)の両辺にそれぞれを掛け、i=1,2,3とおき、それを加えると、
だから、
したがって、(6)と(7)の左辺は等しくなり、
v¹、v²、v³は同時に0でないから、
したがって、となり、λは実数である。
(証明終)
性質2 対称テンソルの異なる固有値に対する固有ベクトルは互いに直交する。
【証明】
(3)の異なる解をλ₁、λ₂に対する固有ベクトルをとすると、
2式の両辺にを掛けて、i=1,2,3とおいてそれぞれ加えれば、
だから両辺の左辺は等しく、
よって、と
は直交する。
(証明終)
性質3 対称テンソルの主値をT¹、T²、T³とすると、
である。
つまり、これらはスカラー(不変量)である。
【証明】
固有方程式を展開すると
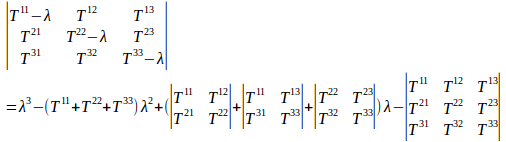
この方程式の解をT¹、T²、T³とすると、
上の2つの方程式の係数を比較すると、
(証明終)
したがって、対称テンソルは
とおくと、
と変形することができる。






