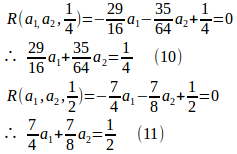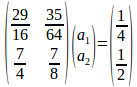誤差の蓄積 [ネコ騙し数学]
誤差の蓄積
の解は
であり、Euler法は(2)式の積分を
と近似し、
を計算し、以下、逐次的に
と計算し、微分方程式(1)の近似解を求める方法である。
特に、
と、等間隔の時、オイラー法は
となる。
そして、(5)の(局所的な)打ち切り誤差はh²程度である。コンピュータを用いる解法では、この打ち切り誤差の他に計算機特有の丸め誤差などが発生するが、丸め誤差は打ち切り誤差と似た性質を持っているので、打ち切り誤差に含めることが可能であろう。
が正確に
であるとき、積分によって得られる
の近似値
の間には
という関係が成立する。ここで、は局所的な打ち切り誤差を表す。
さらに、が誤差
を含めば、
にはこの誤差
の伝播誤差
と局所的な打ち切り誤差
が入る。この2つの誤差によって生じる誤差は、計算をするたびに蓄積し、時に近似計算の結果を無意味なものにしてしまう。
微分方程式(1)、すなわち、y’=f(x,y)のオイラー法による積分(5)において、が正確であれば、
である。
ここで、
が
の誤差を含めば、
右辺第2項をテーラー展開し、は十分小さく高次の項を無視できるとすると、
(10)式を(9)式に代入すると、
![]()
したがって、伝播誤差は
である。
よって、では、
となり、では、
![]()
となる。
のとき、計算を進めるたびに誤差は増大してゆく。そして、
でhが小さければ、
であれば、誤差の影響は積分を繰り返すたびに小さくなり、やがて消失してしまう。
次の微分方程式があるとする。
この微分方程式の解は
である。
(13)式にEuler法を用いると、
となる。
誤差も(14)式に従うとすれば、
したがって、誤差因子1+λhが
すなわち、
であれば、(伝播)誤差は常に一定の範囲に収まる、つまり、有界で、安定である。
λ>0のとき、(16)を満たすことはできないので、(積分の)計算を進めるたびに、伝播誤差が指数関数的に増大する。
参考までに、λ=±1、h=0.1としたときの結果をグラフに示す。
λ=1のとき、誤差が指数関数的に増加していることが分かる。
対して、λ=−1のとき、誤差は0≦x≦1では増加するが、さらに計算が進むに従い、誤差が減少してゆくことが分かる。
また、λh=−2となるように、λ=−2、h=1とすると、次のような振動解が得られる。
そして、λ=−3、h=1とすると、この計算はやがて発散してしまう。
差分法による2階常微分方程式の境界値問題の解法 [ネコ騙し数学]
差分法による2階常微分方程式の境界値問題の解法
次の2階常微分方程式
を、差分法を用いて解く解法について考える。
閉区間[a,b](a≦x≦b)をn等分し
とし、
とおき、さらに分点におけるyの値を
とおく。
(1)式の導関数を
と差分法を用いて近似すると、k=1,2,・・・,n−1において
というn−1本の方程式が得られる。
未知数は、のn−1個なので、連立方程式(4)を解くことにより、これらの未知数を求めることができる。
連立方程式(4)は
とおくと
と書き換えることができる。
そして、(6)式の左辺の係数行列は、3重対角行列なので、TDMA(Tri Diagonal Matrix Algorithm)を用いて解くことができる。
以下に、微分方程式
を解かせたプログラムと、分割数をn=10、n=100とした場合の計算結果を示す。
! 差分法を用いて y''+f(x)y'+g(x)y=h(x) の境界値問題(でぃれくれ型)を解くプログラム
! ただし、固有値問題は解けない!!
parameter (ns=100,ns1=101)
real x(0:ns), y(0:ns)
data x,y/ns1*0.,ns1*0/
n=10
a=0.; b=1. ! 境界のx座標
x(0)=a; x(n)=b
y(0)=2.; y(n)=0. ! 境界条件
call Solver(x,y,n)
write(6,*) ' i x y'
do i=0, n
write(6,100) i, x(i), y(i)
end do
100 format(i3,1x,f9.5,1x,f9.5)
end
function f(x)
f=-14./x
end
function g(x)
g=x**3
end
function h(x)
h=2*x**3
end
! ここより下はいじると危険
! ブラックボックスとして使うべし
subroutine Solver(x,y,n)
real a(n),b(n),c(n),d(n)
real x(0:n), y(0:n)
n1=n-1
dx=(x(n)-x(0))/n
do i=1,n1
x(i)=x(0)+i*dx
end do
! 差分法によって得られる連立方程式の係数の計算
do i=1,n1
a(i)=1-dx/2.*f(x(i))
b(i)=-(2-dx*dx*g(x(i)))
c(i)=1+dx/2.*f(x(i))
d(i)=dx*dx*h(x(i))
end do
d(1)=d(1)-a(1)*y(0) ! 境界条件
d(n1)=d(n1)-c(n1)*y(n) ! 境界条件
call tdma(a,b,c,d,n1) ! TDMAで連立方程式を解く
do i=1,n1
y(i)=d(i) ! 計算結果をセット
end do
end
! TDMA
subroutine tdma(a,b,c,d,n)
real a(n), b(n), c(n),d(n)
do i=1,n-1
ratio=a(i+1)/b(i)
b(i+1)=b(i+1)-ratio*c(i)
d(i+1)=d(i+1)-ratio*d(i)
end do
d(n)=d(n)/b(n)
do i=n-1,1,-1
d(i)=(d(i)-c(i)*d(i+1))/b(i)
end do
end
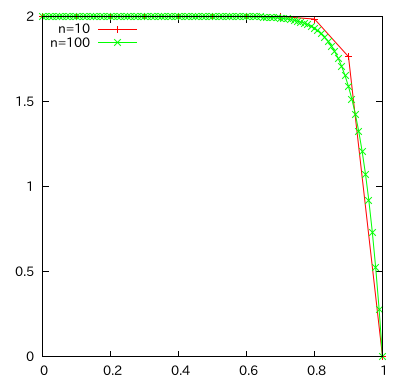
計算結果はおかしく見えるかもしれないけれど、この計算結果は正しいケロよ。
上の微分方程式の解は、ベッセル関数という特殊関数を用いないと表わせないうえに、ベッセル関数は組み込み関数にないので、n=100のときの数値解を厳密解だと考えて欲しいにゃ。
少し違うけれど、十進BASIC用のプログラムは
http://nekodamashi-math.blog.so-net.ne.jp/2016-01-24
に書いてあるので、Fortranを使えないヒト、あるいは、Fortranから他のコンピュータ言語にできないヒトは、コチラのプログラムを参考にしてほしいにゃ。
[境界要素法プログラムを設計する([計算部]の完成)] [ネコ騙し数学]
[境界要素法プログラムを設計する([計算部]の完成)]
1.Free Termの処理
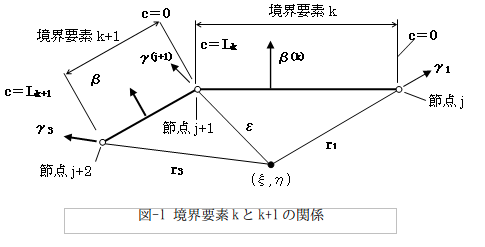
もう一度[内点方程式から境界方程式へ(ラプラス型)]のFree Termの項を考えます。
図-1でε→0の極限を取った場合、式(1)のψ(ξ,η)の(ξ,η)は、節点j+1に一致します。つまりψ(ξ,η)→ψj+1です。よって、
となります。式(2)の最後の形のψj+1の係数の2項目が、境界積分関数で与えられるGam_12です。
節点jが角点の場合、
になるのでした。kj+1は節点j+1の内角です。ところで今は、角点のない解析領域に対応するプログラムを作成中です。節点が角点でない場合、[境界方程式に関する留意点(ラプラス型)]によればkj+1/2/π→1/2におきかえるのが一般的でした。滑らかな境界点の場合、kj+1=πと考えられるからです(β(j+1)=β(j)だから)。
よってメインの「REM 境界要素番号kで境界積分を行うLoop」で全体係数マトリックスA、
を作った後、式(5)のBブロックの対角成分を1/2に上書きする必要があります。上記のLoopの後に、次のコードを追加します。
(「境界要素番号kで境界積分を行うLoop」の後)
REM Bマトリックスの滑らかな境界節点のFree Termを1/2に上書きするLoop
For i = 1 to BN_Count
A(i, i) = 1 / 2
Next i
2.Declare文を追加する
前回の結果より、境界積分のために外部関数Length,Angle,Normal_Param,Normal_Length,Normal_Foot,B_Inte_B1,B_Inte_B2,B_Inte_H1,B_Inte_H2を使用するのでした。これらのDeclare文を追加します。
追加する場所はどこか?という問題があります。個人的な趣味では、これらを使うのは「境界要素番号kで境界積分を行うLoop」なので、道具は「実行者」のすぐそばに置いておきたいのですが、個人的趣味ばかり押し出すと嫌われそうなので(^^;)、普通に[計算部]冒頭に置く事にします。
3.Gauss掃き出し法のサブルーティン名を決める
Gauss掃き出し法のサブルーティン名と引数は、Gauss_0(A, z, n, Zero_Order, Return_Code)としておきます。この名前は趣味です!(←舌の根も乾かぬ内に・・・(^^;))。Gauss_0のDeclare文も[計算部]冒頭に追加します。
A,zの意味はいいと思うので省略します。nは未知数の数(=2*BN_Count),Zero_Orderは正の整数でピボットの0判定条件に使います。つまりピボットの絶対値がEps=10^(- Zero_Order)未満だったら、特異行列です。自分はたいてい、Zero_Order=8を使います。
ピボットの意味がわからなかったら、ネコ先生の記事を読もう!(^^)。
Return_Codeは計算終了時の状態を表し、Return_Code = 0~2の値を取るものとします。Return_Code=0は「正常終了」(ちゃんと連立方程式が解けた)、Return_Code=1は「0の行がある」、Return_Code=2は「特異行列である」だとしておきます。これらはユーザーには関係ないです(プログラマーでないユーザーには(^^))。
だって正常終了しなかったら、開発中のプログラムは間違てるって事ですから。しかし「プログラマー」という、「ユーザーにとっては」まずデバック時に非常に役立ちます(^^)。だからReturn_Codeの値によってはメッセージを出し、無駄な出力も行わないで強制終了するような制御も入れておきましょう。
リリースしたらその制御は発動しない事を願うのみですが、間違って発動したら「旦那、どんなメッセージが出やした?」ってお客さんに犬のようにきけるんですよ(^^)。それは間違い修正やメンテナンスに対する、非常に得難い情報になります。そしてFortranではそのような行為を「旗を立てる」と言いました(^^)。
以上まとめると以下です。
REM [計算部]
External Function Length
External Function Angle
External Function Normal_Param
External Function Normal_Length
External Function Normal_Foot
External Function B_Inte_B1
External Function B_Inte_B2
External Function B_Inte_H1
External Function B_Inte_H2
External Sub Gauss_0
REM 境界要素番号kで境界積分を行うLoop
For i = 1 to BN_Count
REM 特異点番号iの節点iを特定
x0 = BN(i, 1) REM 節点iの(x,y)座標
y0 = BN(i, 2)
For k = 1 to B_Count
REM 要素番号kからEN_B(k,2)に従い節点を特定し、要素ごとに境界積分を実行
j1 = EN_B(k,1) REM 要素kの始端の節点番号
j2 = EN_B(k,2) REM 要素kの終端の節点番号
x1 = BN(j1, 1) REM 節点j1の(x,y)座標
y1 = BN(j1, 2)
x2 = BN(j2, 1) REM 節点j2の(x,y)座標
y2 = BN(j2, 2)
REM (x0,y0),(x1,y1),(x2,y2)から、要素kの境界積分値を計算
REM 積分パラメータ計算
Lk = Length(x1,y1,x2,y2)
r1 = Length(x0,y0,x1,y1)
r2 = Length(x0,y0,x2,y2)
Gam_12 = Angle(x0, y0, x1,y1,x2,y2, r1, r2, Eps)
t = Normal_Param(x0, y0, x1,y1,x2,y2)
h = Normal_Length(x1,y1,x2,y2, t)
s = Normal_Foot(x0, y0, x1,y1,x2,y2, t)
REM ψj1に関する結果をB1,qj1に関する結果をH1で表す
REM ψj2に関する結果をB2,qj2に関する結果をH2で表す
B1 = B_Inte_B1(Lk, r1, r2, Gam_12, h, s, Eps)
B2 = B_Inte_B2(Lk, r1, r2, Gam_12, h, s, Eps)
H1 = B_Inte_H1(Lk, r1, r2, Gam_12, h, s, Eps)
H2 = B_Inte_H2(Lk, r1, r2, Gam_12, h, s, Eps)
REM 上記結果に基づき、係数マトリックスBとHを作成
jj1 = BN_Z(j1,1) REM ψj1の解ベクトルzの中での位置
jjj1 = BN_Z(j1,2) REM qj1の解ベクトルzの中での位置
jj2 = BN_Z(j2,1) REM ψj2の解ベクトルzの中での位置
jjj2 = BN_Z(j2,2) REM qj2の解ベクトルzの中での位置
A(i, jj1) = A(i, jj1) - B1
A(i, jjj1) = A(i, jjj1) + H1
A(i, jj2) = A(i, jj2) - B2
A(i, jjj2) = A(i, jjj2) + H2
Next k
Next i
REM Bマトリックスの滑らかな境界節点のFree Termを1/2に上書きするLoop
For i = 1 to BN_Count
A(i, i) = 1 / 2
Next i
REM 領域要素番号kで領域積分を行うLoop
For i = 1 to BN_Count
REM 特異点番号iの節点iを特定
h = 0
For k = 1 to R_Count
REM 要素番号kからEN_R(k,4)に従い節点を特定し、要素ごとに領域積分を実行
REM 特異点iと要素節点情報から積分値w0を計算
h = h + w0
Next k
REM 上記結果に基づき、既知ベクトルwを作成
z(i) = h
Next i
REM 境界節点番号jで境界条件位置を指定するLoop
For i = BN_Count + 1 to 2 * BN_Count
REM 行番号から節点番号を特定する
j = i - BN_Count
REM 節点番号jからBN_BP(j,2)とBN_Z(j,2) に従い、(D1 D2)ブロックを作成
REM 節点番号jに従いBN_BV(j,2)の値をwブロックの後に並べ、(d1 d2)ブロックを作成
If BN_BP(j,1) = 1 Then
REM ψjが既知が場合
jj = BN_Z(j,1) REM ψjの解ベクトルzの中での位置
A(i, jj) = 1 REM ψjの値を与えるので、Aの成分は1
z(i) = BN_BV(jj,1) REM ψjの値
ElseIf BN_BP(j,2) = 1 Then
REM qjが既知が場合
jj = BN_Z(j,2) REM qjの解ベクトルzの中での位置
A(i, jj) = 1 REM qjの値を与えるので、Aの成分は1
z(i) = BN_BV(jj,2) REM qjの値
End If
Next i
REM 全体係数行列が出来たので、Gaussの掃き出し法にかけ、未知ベクトルzを求める
Zero_Order = 8
Call Gauss_0(A, z, 2 * BN_Count, Zero_Order, Return_Code)
If Return_Code = 0 Then
Print "正常終了しました。"
ElseIf Return_Code = 1 Then
Print "0の行があります。"
End
ElseIf Return_Code = 2 Then
Print "特異行列です。"
End
End If
REM [外部手続き]
REM 境界積分パラメータ ****************************************
External Function Length(x1,y1,x2,y2)
Length = Sqr((x2 - x1)^2 + (y2 - y1)^2)
End Function
External Function Angle(x0, y0, x1,y1,x2,y2, r1, r2, Eps)
If r1 < Eps Then
x01 = 1
y01 = 0
x02 = x2 - x1
y02 = y2 - y1
r1 = 1
ElseIf r2 < Eps Then
x01 = x1 - x2
y01 = y1 - y2
x02 = 1
y02 = 0
r2 = 1
Else
x01 = x1 - x0
y01 = y1 - y0
x02 = x2 - x0
y02 = y2 - y0
End If
Gum_12 = Acos((x01 * x02 + y01 * y02) / r1 / r2)
Sign = Sgn(x01 * y02 - x02 * y01)
Gum_12 = Gum_12 * Sign
Angle = Gum_12
End Function
External Function Normal_Param(x0, y0, x1,y1,x2,y2)
a = x2 - x1
b = y2 - y1
t = (b * (x1 - x0) - a * (y1 - y0)) / (a^2 + b^2)
Normal_Param = t
End Function
External Function Normal_Length(x1,y1,x2,y2, t)
a = x2 - x1
b = y2 - y1
h = Abs(t) * Sqr(a^2 + b^2)
Normal_Length = h
End Function
External Function Normal_Foot(x0, y0, x1,y1,x2,y2, t)
a = x2 - x1
b = y2 - y1
s = Sqr((t * b + x0 - x1)^2 + (-t * a + y0 - y1)^2)
Normal_Foot = s
End Function
REM 境界積分 **********************************************
External Function B_Inte_B1(Lk, r1, r2, Gam_12, h, s, Eps)
If r1 < Eps Then
B1 = Gam_12 / 2 /Pai
ElseIf r2 < Eps Then
B1 = 0
Else
B1 = Gum_12 - 1 / Lk * (s * Gum_12 + h * (Log(r2) - Log(r1)))
B1 = B1 / 2 /Pai
End If
B_Inte_B1 = B1
End Function
External Function B_Inte_B2(Lk, r1, r2, Gam_12, h, s, Eps)
If r1 < Eps Then
B2 = 0
ElseIf r2 < Eps Then
B2 = Gam_12 / 2 /Pai
Else
B2 = 1 / Lk * (s * Gum_12 + h * (Log(r2) - Log(r1)))
B2 = B1 / 2 /Pai
End If
B_Inte_B2 = B2
End Function
External Function B_Inte_H1(Lk, r1, r2, Gam_12, h, s, Eps)
If r1 < Eps Then
H1 = Lk / 4 / Pai * (Log(Lk) - 3 / 2)
ElseIf r2 < Eps Then
H1 = Lk / 4 / Pai * (Log(Lk) - 1 / 2)
Else
H1 = -1 / 4 / Pai / Lk * (r2^2 * Log(r2) - r1^2 * Log(r1) - 1 / 2 *((Lk - s)^2 - s^2))
H1 = H1 + 1 / 2 / Pai * (1 - s / Lk) * (h * Gum_12 + (Lk - s) * Log(r2) + s * Log(r1) - Lk)
End If
B_Inte_H1 = H1
End Function
External Function B_Inte_H2(Lk, r1, r2, Gam_12, h, s, Eps)
If r1 < Eps Then
H2 = Lk / 4 / Pai * (Log(Lk) - 1 / 2)
ElseIf r2 < Eps Then
H2 = Lk / 4 / Pai * (Log(Lk) - 3 / 2)
Else
H2 = 1 / 4 / Pai / Lk * (r2^2 * Log(r2) - r1^2 * Log(r1) - 1 / 2 *((Lk - s)^2 - s^2))
H2 = H2 + 1 / 2 / Pai * s / Lk * (h * Gum_12 + (Lk - s) * Log(r2) + s * Log(r1) - Lk)
End If
B_Inte_H2 = H2
End Function
REM Gauss掃き出し法 **********************************************
External Sub Gauss_0(A, z, Zero_Order, Return_Code)
REM まだ何にもしない
End Sub
ガラーキン法 [ネコ騙し数学]
微分方程式
境界条件を
とする。
ここで、Vは微分方程式が定義されている領域で、Sは境界面とする。
(1)の解u(x)が独立な試行関数(基底関数)を用いて
と近似できるとする。
このとき、
を残差といい、R=0のときは解uと一致する。
(3)に重みを掛け、
となるようを定める方法が有限要素法の重み付き残差法である。
この重みにディラックのδ関数
を用いるものが選点法である。
この重みに試行関数
、すなわち、
とする方法がガラーキン法である。
例によって、微分方程式
を、がラーキン法を用いて解くことにする。
この微分方程式の近似解を
とすると、試行関数は
となり、残差は
となる。
したがって、
また、
したがって、
よって、
になる。
ガラーキン法による計算結果は次の通り。比較のために、選点法による計算結果も示してある。
厳密解との差は殆ど無いので、グラフでは厳密解とほとんど重なってしまう。
この他に最小2乗法、モーメント法などがあるけれど、あくまで一般論ですが、有限要素法の中ではガラーキン法がもっとも精度がよいといわれている。
[境界要素法プログラムを設計する(境界積分サブルーティン:実装編)] [ネコ騙し数学]
[境界要素法プログラムを設計する(境界積分サブルーティン:実装編)]
1.積分パラメータ関数の実装
前々回、メインの中に与えた境界積分サブルーティン(関数)は、以下でした。
REM (x0,y0),(x1,y1),(x2,y2)から、要素kの境界積分値を計算
REM ψj1に関する結果をB1,qj1に関する結果をH1で表す
REM ψj2に関する結果をB2,qj2に関する結果をH2で表す
Lk = Length(x1,y1,x2,y2)
Beta_k = Angle(x2 - x1, y2 - y1, Lk)
r1 = Length(x0,y0,x1,y1)
r2 = Length(x0,y0,x2,y2)
Gamm_1 = Angle(x1 - x0, y1 - y0, r1)
Gamm_2 = Angle(x2 - x0, y2 - y0, r2)
h = Normal_Length(x2 - x1, y2 - y1, x0,y0)
s = Normal_Foot(x2 - x1, y2 - y1, x0,y0, h)
B1 = B_Inte_B1(Lk, r1, r2, Beta_k, Gamm_1, Gamm_2, h, s)
B2 = B_Inte_B2(Lk, r1, r2, Beta_k, Gamm_1, Gamm_2, h, s)
H1 = B_Inte_H1(Lk, r1, r2, Beta_k, Gamm_1, Gamm_2, h, s)
H2 = B_Inte_H2(Lk, r1, r2, Beta_k, Gamm_1, Gamm_2, h, s)
最初にLength関数ですが、明らかに次でOKです。
External Function Length(x1,y1,x2,y2)
Length = Sqr((x2 - x1)^2 + (y2 - y1)^2)
End Function
前々回に予告したように、関数とサブルーティンはローカル変数を持てる、外部手続きで統一します。Normal_LengthとNormal_Footの計算に疑問の余地はないのですが、ちょっと長そうなので後にします。
次にBeta_kの扱いですが、前回の検討からGamm_1,Gamm_2の特殊ケースとして扱って良いとわかりました。という訳でGamm_1とGamm_2の計算です。これらは単独に計算しては駄目で、Gamm_2-Gamm_1の形で計算する必要がありました。それをGam_12で表します。
まず特異点(x0,y0)が要素節点(x1,y1)と(x2,y2)に一致しないケースから考え始めると、わかりやすいと思います。以下、前回を参照しつつ・・・。
計算開始の前提として、図-1のr1,r2および(x0,y0),(x1,y1)と(x2,y2)は引数渡しされるとします。また特異点と要素節点の一致/不一致判定のために、0距離判定値Epsも必要です。
External Function Angle(x0, y0, x1,y1,x2,y2, r1, r2, Eps)
If r1 < Eps Then
x01 = 1
y01 = 0
x02 = x2 - x1
y02 = y2 - y1
r1 = 1
ElseIf r2 < Eps Then
x01 = x1 - x2
y01 = y1 - y2
x02 = 1
y02 = 0
r2 = 1
Else
x01 = x1 - x0
y01 = y1 - y0
x02 = x2 - x0
y02 = y2 - y0
End If
Gum_12 = Acos((x01 * x02 + y01 * y02) / r1 / r2)
Sign = Sgn(x01 * y02 - x02 * y01)
Gum_12 = Gum_12 * Sign
Angle = Gum_12
End Function
r1 < Eps(r1=0)の時は、(x01,y01)=(1,0)とするのでした。この時(x0,y0)は(x1,y1)に一致するとみなせるので、(x02,y02)=(x2 - x1,y2 - y1)です。そしてr1=1とします。
r2 < Eps(r2=0)の時は、(x02,y02)=(1,0)とするのでした。この時(x0,y0)は(x2,y2)に一致するとみなせるので、(x01,y01)=(x1 - x2,y1 - y2)です。そしてr2=1とします。
以上より、積分パラメータを与える関数呼び出しは、
Lk = Length(x1,y1,x2,y2)
r1 = Length(x0,y0,x1,y1)
r2 = Length(x0,y0,x2,y2)
Gam_12 = Angle(x0, y0, x1,y1,x2,y2, r1, r2, Eps)
h = Normal_Length(x0, y0, x1,y1,x2,y2)
s = Normal_Foot(x0, y0, x1,y1,x2,y2)
になります(Normal_Length,Normal_Footの引数が前回のままでは不味いと気付いた(^^;))。
Normal_Lengthの実装は以下です。Normal_Lengthは図-1の垂線距離hを求めます。
a = x2 - x1
b = y2 - y1
とすると、(x1,y1)と(x2,y2)を通る直線は、y=b/a*xに平行です。a=0の場合も考慮して、これをbx-ay=0の形にし、(x1,y1)を通る事を考慮すると要素kの直線の方程式は、b(x-x1)-a(y-y1)=0になります(なんか受験を思い出すなぁ~(^^))。直線の式からその垂線ベクトルの方位は、明らかに(b,-a)です。従って点(x0,y0)からの垂線は、tを任意の実数として、
と書けます。(1)がb(x-x1)-a(y-y1)=0に載る条件は、(1)を代入し、
(2)をtについて解くと、
従ってhは、tが(3)の値の時、
tを利用すれば垂線の足もわかるので、図-1のsも出せます。垂線の足の座標は、tを(3)の値にした(1)です。よってsは、
から、
です。
こうなるとNormal_LengthとNormal_Footで同じパラメータtを利用したいですよね。こうしましょう。
h = Normal_Length(x1,y1,x2,y2, t)
s = Normal_Foot(x0, y0, x1,y1,x2,y2, t)
External Function Normal_Param(x0, y0, x1,y1,x2,y2)
a = x2 - x1
b = y2 - y1
t = (b * (x1 - x0) - a * (y1 - y0)) / (a^2 + b^2)
Normal_Param = t
End Function
External Function Normal_Length(x1,y1,x2,y2, t)
a = x2 - x1
b = y2 - y1
h = Abs(t) * Sqr(a^2 + b^2)
Normal_Length = h
End Function
External Function Normal_Foot(x0, y0, x1,y1,x2,y2, t)
a = x2 - x1
b = y2 - y1
s = Sqr((t * b + x0 - x1)^2 + (-t * a + y0 - y1)^2)
Normal_Foot = s
End Function
2.境界積分関数の実装
以上で境界積分に必要な積分パラメータは全て揃いました。
B1 = B_Inte_B1(Lk, r1, r2, Gam_12, h, s, Eps)
B2 = B_Inte_B2(Lk, r1, r2, Gam_12, h, s, Eps)
H1 = B_Inte_H1(Lk, r1, r2, Gam_12, h, s, Eps)
H2 = B_Inte_H2(Lk, r1, r2, Gam_12, h, s, Eps)
で良いはずです。引数の最後にEpsが入るのは、これらでも特異点と要素節点の一致/不一致判定が必要だからです。
後はB_Inte_?の中に、[内点方程式の積分公式(ラプラス型)]と[内点方程式から境界方程式へ(ラプラス型)]で導出した式を並べるだけですが、関数の内部構造はExternal Function Angleと同一構造になるとわかります。なのでIfブロックの形を決め、「関数名 = 値」の行を書いてから、計算式を並べる事をお奨めします。
External Function B_Inte_B1(Lk, r1, r2, Gam_12, h, s, Eps)
If r1 < Eps Then
B1 = Gam_12 / 2 /Pai
ElseIf r2 < Eps Then
B1 = 0
Else
B1 = Gum_12 - 1 / Lk * (s * Gum_12 + h * (Log(r2) - Log(r1)))
B1 = B1 / 2 /Pai
End If
B_Inte_B1 = B1
End Function
External Function B_Inte_B2(Lk, r1, r2, Gam_12, h, s, Eps)
If r1 < Eps Then
B2 = 0
ElseIf r2 < Eps Then
B2 = Gam_12 / 2 /Pai
Else
B2 = 1 / Lk * (s * Gum_12 + h * (Log(r2) - Log(r1)))
B2 = B1 / 2 /Pai
End If
B_Inte_B2 = B2
End Function
External Function B_Inte_H1(Lk, r1, r2, Gam_12, h, s, Eps)
If r1 < Eps Then
H1 = Lk / 4 / Pai * (Log(Lk) - 3 / 2)
ElseIf r2 < Eps Then
H1 = Lk / 4 / Pai * (Log(Lk) - 1 / 2)
Else
H1 = -1 / 4 / Pai / Lk * (r2^2 * Log(r2) - r1^2 * Log(r1) - 1 / 2 *((Lk - s)^2 - s^2))
H1 = H1 + 1 / 2 / Pai * (1 - s / Lk) * (h * Gum_12 + (Lk - s) * Log(r2) + s * Log(r1) - Lk)
End If
B_Inte_H1 = H1
End Function
External Function B_Inte_H2(Lk, r1, r2, Gam_12, h, s, Eps)
If r1 < Eps Then
H2 = Lk / 4 / Pai * (Log(Lk) - 1 / 2)
ElseIf r2 < Eps Then
H2 = Lk / 4 / Pai * (Log(Lk) - 3 / 2)
Else
H2 = 1 / 4 / Pai / Lk * (r2^2 * Log(r2) - r1^2 * Log(r1) - 1 / 2 *((Lk - s)^2 - s^2))
H2 = H2 + 1 / 2 / Pai * s / Lk * (h * Gum_12 + (Lk - s) * Log(r2) + s * Log(r1) - Lk)
End If
B_Inte_H2 = H2
End Function
以上の結果は、[計算部]と[外部手続き]のところへは、まだはめ込みません。[計算部]では、まだやる事があるからです(もぉ~、境界要素法って面倒くさいなぁ~(^^;))。
2階常微分方程式の境界値問題を選点法で解く2 [ネコ騙し数学]
2階常微分方程式の境界値問題を選点法で解く2
問題 次の微分方程式を解け。
【答】
前回、この微分方程式の解を
と近似し、残差
をとし、重み関数wにディラックのデルタ関数
をとり、
となるようにを定める有限要素法の選点法を用い、選点を1/2とすることにより、
という近似解を得た。
しかし、こうして得た近似解の誤差が大きかったので、より精度のよい近似解を求める方法を考える。
そこで、(1)式を
とおくと、
となる。
このとき、
となるので、残差は
となる。
未知数がa₁、a₂の2つなので、これを定めるために選点をx=1/4とx=1/2に選び、その位置での残差を0とすると、
(10)と(11)から
という連立方程式が得られ、これを解くと、
となり、
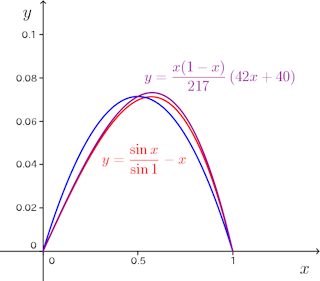
という近似解が得られる。
(12)は(6)よりも厳密解(1)からの乖離が小さくなり、(1)の挙動をよく捉えていることが分かる。
(9)式の
とおくと、
と表すことができる。このψ₁、ψ₂を試行関数(Trial Function)と呼ぶ。
さらに、
とおくと、微分方程式は
と書くことができ、残差は
で表すことができる。
より一般に書くと、
これに重み関数をかけ、
となるように、この連立方程式(15)から、未知数を定め、微分方程式(13)の近似解を有限要素法の重み付き残差法という。
この重み関数のディラックのデルタ関数
を用いるものを選点法といい、デルタ関数の性質から
になる。
n=2のとき、未知数はa₁、a₂の2つだから、点をx₁、x₂の2点を選び、連立方程式
を解くことによって、a₁、a₂を定めることができる。
これが計算の仕組みというわけ。
[境界要素法プログラムを設計する(境界積分サブルーティン:具体調査編)] [ネコ騙し数学]
[境界要素法プログラムを設計する(境界積分サブルーティン:具体調査編)]
1.最後はボトムアップになる
例は1個で十分です。
式(1)は、[内点方程式の積分公式(ラプラス型)]であげた、境界要素kの節点jのψjの係数を与える積分結果です(ずいぶん前のような気がしてますが(^^;))。特異点が要素節点に一致しない場合、境界方程式でもこの形の計算は必ずします。というかこういう場合の方が、圧倒的に多いです。
式中のLk,s,γ2,γ1,h,r2,r1が図-1から定められる積分パラメータです。このうちLk,s,h,r2,r1は単純に計算できます。例えばr1なら明らかに、
ですし、s,hはちょっと手がかかりますが、基本は(x0,y0),(x1,y1),(x2,y2)で係数が決まる2行2列の連立方程式を解くだけです。問題はγ2,γ1の与え方です。これは一見簡単そうに見えます。例えばγ1なら、
でいいんでないの?と。まず汎用言語の数学関数のAtn(tan-1の事)は、値域がふつう-π/2~π/2です。なんか鬱陶しそうだから、x1-x0とy1-y0の符号に注意して場合分けすれば、容易に0~2πをカバーできます。これでγ2-γ1>0は容易に計算できそうです。でも図-2のような場合はどうしますか?。
Atnを0~2πをカバーできるように改造したとしても、図-2では明らかにγ2<γ1でγ2-γ1<0です。しかし線積分(境界積分)は常に左回りなので、図中の角度矢印で示したように(左回り)、γ2-γ1>0でなければならず、しかも0~2πで表した|γ2-γ1|は本当の(γ2-γ1)と値が違います(2π大きい)。
では境界要素がx軸方向を横切る時だけ、2π引いて符号を反転させればOKなのか?というと、一般的には図-2への対処も必要です。
この場合は角度矢印が示すように(右回り)、γ2-γ1<0が正解です。図-3では0~2πの角度定義でたまたまγ2<γ1なので、そのままやって正解になりますが、図-2と3の複合ケースは?。・・・もう鬱陶しくてやってられません(^^;)。
つまりγ1とγ2は(βkも)単独で計算しては駄目なんですよ。あくまでγ1とγ2の角度差分を局所情報に基づいて計算する必要があります。こういう事は、普通の積分では起こりません。普通は図-1のように一周したら値は元に戻って問題ないはずです。これは積分結果がtan-1になるような正則でない関数を積分せざる得ない、特異積分を使っている境界要素法の特徴の反映です(複素積分を知ってる人なら、イメージできるはず)。そういう事情から、前回メインで大雑把に決めた関数の引数並びも、角度差分を与えるように変更する必要があります。
これはボトムアップです。このように最後はボトムアップになる事は多いです。トップダウンだけでは問題の個別状況の全ては把握できないからです。でも最後までボトムアップは我慢した方が、たいてい上手く行きます。
2.角度差分を計算するアルゴリズムを考える
一つだけ確かなのは、|γ2-γ1|はπ以下だ、という点です。|γ2-γ1|がπに成り得るのは、特異点が境界要素の中点上などにある場合なので、πを越える事はありません。そうすると格好の数学関数があります。Acos(cos-1)です。Acosの値域は、汎用言語においてたいてい0~πです。内積の定義から、
として、
なので
と求められます。|γ2-γ1|の符号は要するに、図-2,3の角度矢印の向きがわかれば良いので、ベクトル(x01,y01)と(x02,y02)の外積を利用する手があります。(x01,y01)はγ1方向,(x02,y02)はγ2方向のベクトルなので。(x01,y01)と(x02,y02)を3次元化して外積を取ると、
になります。(7)右辺のz成分が+なら左回りで、γ2-γ1=|γ2-γ1|。(7)右辺のz成分が-なら右回りで、γ2-γ1=-|γ2-γ1|と判定できます。ただし式(6)と(7)は小さすぎるr1やr2に対しては、結果が不安定になるのは目に見えています。本当にr1やr2が0なら、division by zeroエラーになります。なりますが、特異点が要素節点に一致する場合も、もともと扱うのでした。だとすればそういう特殊ケースは、特異点が要素節点に一致するケースに含めれば十分です。
3.特異点が要素節点に一致するケース
ここでもγ2-γ1の扱いが問題になります。[内点方程式から境界方程式へ(ラプラス型)]でFree Termの項は、次のように計算されました。
式(8)上段の1/2π×()内の1項目が要素k+1のγ2-γ1すなわち、図-4のγ3-γ(j+1)です。2項目は要素kのγ2-γ1すなわち、図-4のγ(j+1) -γ1です。ただしε→0の極限で考えてます。
でも待って下さい。ε→0の場合(特異点が要素節点に一致する場合)、どうやってγ(j+1) を与えれば良いんでしょう?。だって数値計算上はε=0なんですから。そしてすぐに気づくのは、特異点が要素節点に一致するケースでは、「個々の要素の境界積分値は、特異点の要素節点への近づき方に依存する!」という驚愕の事態が発覚します。もろな特異積分!。境界積分は結局、可積分でない?(^^;)。
・・・とけっこう猛烈に焦っちゃう訳ですが、式(8)下段では不定なγ(j+1)が引き算でキャンセルされて、「境界積分全体では近づき方に依存せず、値は一意に定まる」事になります。境界要素法は、こういう危ういところを持っています。ブレビアさんがなりふり構わず、コーシーの主値積分を持ち込んだ気持ちもわかりますよ(^^;)。
つまり足せばγ(j+1)は消えるのですから、逆に言えばなんでも良い訳です。例えば要素kで(x02,y02)=(1,0)とし、要素k+1でも(x01,y01)=(1,0)にするとか。共有節点でγの方法が揃ってればOKなはず。どうしてかと言うと特異積分値は、局所情報に基づいて計算する必要があるから。
特異点が要素節点に一致するケースでは、その点でγ1,γ2は(1,0)方向に取ると決定します。後で後悔するかも知れませんが(^^;)。
あと考えるべき事は、r1またはr2がどれくらい0に近かったら、0とみなすかです。これは【桁落ち誤差と丸め誤差はプログラマーの敵!】のところで書いたように、
http://nekodamashi-math.blog.so-net.ne.jp/archive/c2306081239-2
「問題のスケール規模」で決めるのが妥当と考えられます。r1,r2は特異点と要素節点の距離です。これに対応するスケール規模は明らかに、解析領域の大きさです。0判定Epsはどこで与えれば良いでしょう?。
手がかりはたいてい「実行者」と「妥当な実行タイミング」にあります。「実行者」の第一候補は[入力部]です。[入力部]のRoll(役割)は、解析領域という外部情報をセットし[計算部]へ渡す事です。Epsは解析領域の大きさで決まるので、これは外部情報のセットです(そして渡す)。
次に実行タイミングですが、Epsのセットは[計算部]の実行前に、事前に一回だけで十分です。[計算部]の実行前には、[入力部]の実行があります。「実行者」と「妥当な実行タイミング」が理想的に一致したので、[入力部]の中でEpsのセットを行います。セットの場所は、全ての入力が完了した後の方がなんか安心じゃないですか?。
[メモ欄]と[宣言部]はできれば一対一に対応させたいので、[メモ欄]の最後に「REM Eps:0判定,Eps0:0オーダー」を追加し、[宣言部]の最後には「REM Eps:0判定」と「Eps0 = 10^(-6) REM 0オーダー」のコードを追加します。コードの心は、解析領域の大きさの1/100万より小さい距離は0とみなすです。そして[入力部]の最後に、
REM 全ての入力完了
REM 解析領域のx方向幅とy方向幅を取得
x_Min = 10^10 REM x座標最小値初期化
x_Max = -10^10 REM x座標最大値初期化
y_Min = 10^10 REM y座標最小値初期化
y_Max = -10^10 REM y座標最大値初期化
For j = 1 to BN_Count
h = BN(j, 1) REM j節点のx座標
If h < x_Min Then
x_Min = h
End If
If x_Max < h Then
x_Max = h
End If
h = BN(j, 2) REM j節点のy座標
If h < y_Min Then
y_Min = h
End If
If y_Max < h Then
y_Max = h
End If
Next j
x_Width = x_Max - x_Min REM 解析領域のx方向幅
y_Width = y_Max - y_Min REM 解析領域のy方向幅
REM 0判定距離をセット
If x_Width < y_Width Then
Eps = y_Width * Eps0
Else
Eps = x_Width * Eps0
End If
このEpsの与え方は、解析領域の最大幅をスケール規模とするやり方です。これでは駄目な場合ももちろんあり得ますが、とりあえず(^^;)。今回は[メモ欄][宣言部][入力部]のみあげます。[計算部]は、引数並びから検討し直す必要があるとわかったので。
ところでもう一個忘れてました。式(1)を見ると、定数πも必要です。これも[メモ欄]と[宣言部]に追加しておきます。
※ 後で調べてみたら、MAX関数とMIN関数と定数PIが組み込みになってました。まぁ~、好きにして下さい(^^;)。
REM [メモ欄]
REM B_Count:境界要素数
REM EN_B(k,2):境界要素-節点対応表,k=1~B_Count
REM (k,1):要素kの始端の節点No.,(k,2):終端の節点No.
REM R_Count:領域要素数
REM EN_R(k,4):領域要素-節点対応表,k=1~R_Count
REM (k,j),j=1~4:jに従って要素kの要素節点No.を左回りに格納
REM BN_Count:境界節点数
REM BN(j,2):境界節点座標,j=1~BN_Count,(j,1):節点jのx座標,(j,2):y座標
REM RN_Count:領域節点数
REM RN(j,2):領域節点座標,j=1~RN_Count,(j,1):節点jのx座標,(j,2):y座標
REM BN_BP(j,2):節点の境界条件の有無,j=1~BN_Count
REM (j,1):節点jのψjが既知なら1、そうでないなら0
REM (j,2):節点jのqjが既知なら1、そうでないなら0
REM BN_BV(j,2):境界条件の値,j=1~BN_Count
REM (j,1):節点jのψjに与える値
REM (j,2):節点jのqjに与える値
REM z(i):未知ベクトル,i=1~2*BN_Count
REM BN_Z(j,2):節点-未知数対応表,j=1~BN_Count
REM (j,1):ψjのzの中の位置,(j,2):qjのzの中の位置
REM 節点j→ψj→z(j),節点j→qj→z(BN_Count+j)
REM A(i, j):全体係数マトリックス、i,j=1~2*BN_Count
REM Eps:0判定
REM Eps0:0オーダー
REM Pai:π
REM [宣言部]
REM 配列寸法の上限は1000
REM B_Count:境界要素数
REM R_Count:領域要素数
Dim EN_B(1000,2) REM 境界要素-節点対応表,k=1~B_Count
Dim EN_R(1000,4) REM 領域要素-節点対応表,k=1~R_Count
REM BN_Count:境界節点数
REM RN_Count:領域節点数
Dim BN(1000,2) REM 境界節点座標,j=1~BN_Count
Dim RN(1000,2) REM 領域節点座標,j=1~RN_Count
Dim BN_BP(1000,2) REM 節点の境界条件の有無,j=1~BN_Count
Dim BN_BV(1000,2) REM 境界条件の値,j=1~BN_Count
Dim BN_Z(1000,2) REM 節点-未知数対応表,j=1~BN_Count
Dim z(1000) REM 未知ベクトル,i=1~2*BN_Count
Dim A(1000, 1000) REM 全体係数マトリックス、i,j=1~2*BN_Count
REM Eps:0判定
Eps0 = 10^(-6) REM 0オーダー
Pai = Acos(-1) REM π:Fortranになじんだ人なら、懐かしくて泣いちゃう式(^^)
REM [入力部]
REM境界要素数B_Countと領域要素数R_Countは、事前に与えられると仮定する。
REM 境界要素と領域要素データは、要素ごとに節点番号が与えられると仮定する。
REM 与えられる節点番号は、左回りに順序付けられたものが与えられると仮定する。
REM 境界要素を要素番号kで読み込むLoop
REM Loop内で要素ごとの節点番号を読み、境界要素-節点対応表EN_B(k,2)をセット
For k = 1 to B_Count
EN_B(k,1) = ?
EN_B(k,2) = ?
Next k
REM 領域要素を要素番号kで読み込むLoop
REM Loop内で要素ごとの節点番号を読み、領域要素-節点対応表EN_R(k,4)をセット
For k = 1 to R_Count
For j = 1 to 4
EN_R(k,j) = ?
Next j
Next k
REM境界節点数BN_Countと領域節点数RN_Countは、事前に与えられると仮定する。
REM 境界節点を節点番号jで読み込むLoop
REM Loop内で境界節点座標を読み、BN(j,2)をセット
For j = 1 to BN_Count
BN(j,1) = ?
BN(j,2) = ?
Next j
REM 領域節点を節点番号jで読み込むLoop
REM Loop内で領域節点座標を読み、RN(j,2)をセット
For j = 1 to RN_Count
RN(j,1) = ?
RN(j,2) = ?
Next j
REM 境界条件の場所を節点番号jで読み込むLoop
REM Loop内で節点jの境界条件の有無を読み、BN_BP(j,2)をセット
For j = 1 to BN_Count
BN_BP(j,1) = ?
BN_BP(j,2) = ?
Next j
REM 境界条件の値を節点番号jで読み込むLoop
REM Loop内で節点jの境界条件の値を読み、BN_BV(j,2)をセット
For j = 1 to BN_Count
BN_BV(j,1) = ?
BN_BV(j,2) = ?
Next j
REM 節点番号jのLoopで、節点-未知数対応表BN_Z(j,2)をセット
REM (j,1):ψjのzの中の位置,(j,2):qjのzの中の位置
REM 対応は、節点j→ψj→z(j),節点j→qj→z(BN_Count+j)
For j = 1 to BN_Count
BN_Z(j,1) = j
BN_Z(j,2) = BN_Count + j
Next j
REM 全ての入力完了 **********************************************
REM 解析領域のx方向幅とy方向幅を取得
x_Min = 10^10 REM x座標最小値初期化
x_Max = -10^10 REM x座標最大値初期化
y_Min = 10^10 REM y座標最小値初期化
y_Max = -10^10 REM y座標最大値初期化
For j = 1 to BN_Count
h = BN(j, 1) REM j節点のx座標
If h < x_Min Then
x_Min = h
End If
If x_Max < h Then
x_Max = h
End If
h = BN(j, 2) REM j節点のy座標
If h < y_Min Then
y_Min = h
End If
If y_Max < h Then
y_Max = h
End If
Next j
x_Width = x_Max - x_Min REM 解析領域のx方向幅
y_Width = y_Max - y_Min REM 解析領域のy方向幅
REM 0判定距離をセット
If x_Width < y_Width Then
Eps = y_Width * Eps0
Else
Eps = x_Width * Eps0
End If
有限要素法の選点法で、2階常微分方程式の境界値問題を解く [ネコ騙し数学]
有限要素法の選点法で、2階常微分方程式の境界値問題を解く
問題1 次の微分方程式の解を求めよ。
【解】
この微分方程式の特性方程式は
したがって、この微分方程式の基本解はだから、一般解は
である。
境界条件より
これを解くと、
したがって、
(解答終)
これを差分で解くのは芸がないということで、有限要素法の選点法を用いてこの微分方程式を解くことにする。
それに先立ち、問題の微分方程式を
と置き換え、問題の微分方程式をzの微分方程式に書き換えると、
になる。
こんとき、この微分方程式の境界条件は
となる。
そこで、この境界条件を満たす関数
を近似解と仮定するケロ。
そこで、(2)のzをuに置き換えた
を残差と呼ぶことにする。
もしuが(2)の解であれば、残差は0。しかし、(3)は(2)の解ではないので、R≠0である。
ここで、
となるように重み関数w(x)を調整し、(5)の積分の値が0になるようにする。
そして、(5)を満足する(3)を微分方程式(2)の近似解としようじゃないか。
この重み関数にδ関数
なるナゾの関数を採用し、(5)の積分を行うと
になる。
さてさて、
したがって、
x₀=1/2とすると、(6)より
で、
だから
に違いない。
赤線が厳密解の
青線が
この微分方程式に関する限り、厳密解との差は殆どないという驚きの結果が得られる。
1/3を選点x₀に選ぶと、
したがって、
よって、
この微分方程式の場合、1/2にとったほうが1/3にとったほうが精度がよいことが分かる。
このように微分方程式の解を求める方法を選点法という。
問題2 次の微分方程式を解け。
【解】
同次方程式
の特性方程式は、
したがって、同次方程式の一般解は
特殊解y₀は
したがって、この微分方程式の一般解は
である。
境界条件x=0のときy=0より
x=1のときy=0より
よって、
(解答終)
この微分方程式の場合も同様に
とおくと、
となる。
そこで、x=1/2にとると、
したがって、
粗い近似だから合うほうがおかしいケロよ。そこで、精度をあげる方法を考えることにするにゃ。
ホイン(Heun)法 [ネコ騙し数学]
ホイン(Heun)法
§1 オイラー法
微分方程式
の解は
である。
(2)式の右辺の積分を
で近似すると、(2)式は
と近似することにより、x₀を計算の起点とし、x₁、x₂、・・・と築時的に計算をすることができる。
とあらわすことにすると、
になる。
とくに、点が等間隔hに並んでいるとき、
である。
この方法をオイラー法という。
問題 オイラー法を用いて、次の微分方程式のx=0.1、0.2、0.3におけるyの値を求めよ。
【解】
x₀=0、y₀=y(x₀)=1、h=0.1とおくと、
x₁=0.1、y₁=1.05だから
x₂=0.2、y₂=1.163だから
したがって、
x=0.1のとき、y=1.05
x=0.2のとき、y=1.1106
x=0.3のとき、y=1.1846
(解答終)
表計算ソフトを用いた計算結果を以下に示す。
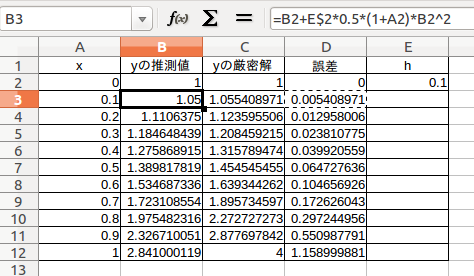
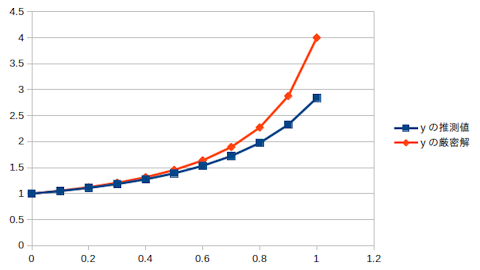
オイラー法だと、計算を進めると、誤差が蓄積して、その結果、厳密解
との食い違いが大きくなっていくことが理解できると思う。
§2 ホイン法
まず、オイラー法
を用いてを計算し、次に台形公式
と修正する。
以下同様に、所定の精度が得られるまで
と反復計算をする方法をホイン法という。
ホイン法を用いて、問題の微分方程式をh=0.1と同一の条件で解いた結果は次の通り。
この計算に用いたプログラムは以下の通り。
#include <stdio.h>
#include <math.h>
double f(double x, double y) {
return 0.5*(1+x)*y*y;
}
void Heun(double *x , double *y , double h , int n) {
double eps = 1.0e-6, err;
double yn = 0.;
int i,j, limit = 100;
for(i=0; i< n; i++) {
x[i+1]=x[i]+h;
// Euler法で予備計算
y[i+1] = y[i] + h*f(x[i],y[i]);
for (j=1; j <= limit; j++) { // 所定の精度が得られるまで反復
// 台形公式で修正
yn = y[i]+0.5*(f(x[i],y[i])+f(x[i+1],y[i+1]))*h;
err =fabs(y[i+1]-yn);
if (err <= eps) break;
// y[i+1]の更新
y[i+1]=yn;
}
}
}
double Exact(double x) {
return 4./(4 - 2*x -x*x);
}
main() {
double x[11], y[11];
double h;
int i, n;
h=0.1;
n=10;
for (i = 0; i<=n; i++) {
x[i] = 0; y[i]=0;
}
x[0]=0; y[0]=1.; // xとyの初期値
Heun(x,y,h, n); // Heun法を呼び出す
printf(" x y(Heun) y(exact) error(%) \n");
for (i=0; i <= n; i++) {
printf("%f %f %f %f\n", x[i],y[i],Exact(x[i]),fabs(1.0-y[i]/Exact(x[i]))*100);
}
}
オイラー法より、Heun(予測修正子法ともいう)のほうが精度よく計算できていることがわかるだろう。
数値計算の誤差:打ち切り誤差と丸め誤差 [ネコ騙し数学]
数値計算の誤差:打ち切り誤差と丸め誤差
f(x)は何回でも微分可能な関数とする。
このとき、f(a+h)はx=aにおいて次のようにテーラー展開が可能である。
有限項で打ち切れば、
は剰余項であり、有限項で打ち切ったときの誤差に相当する。
最も簡単なa=0のときを考えてみる。
かりに
という関数があるとする、
だから、これをx=0でテーラー展開(マクローリン展開)すると、
と一致する。
有限な多項式で表される関数ならば、上の例のように第n次以下の導関数を求めることによってその係数を求めることができる。しかし、テーラー展開(マクローリン展開)が指数関数のように、
と無限級数になる場合、これを無限に計算することはできないので、適当な次数nで打ち切って計算をしなければならない。
たとえば、3次の以上の項を落とせば、
そして、その誤差、打ち切り誤差O(x³)は
と評価されるであろう。
この他に、有限桁の数しか扱えないコンピュータの計算誤差には、丸め誤差と呼ばれるものがある。
たとえば、10進数の0.1は2進数で書くと
という無限小数、循環小数になってしまう。
したがって二進数の小数点8桁で打ち切ると0.00011001(二進数)となる。この0.00011001(二進数)を十進数に直すと0.09765625(十進数)となるので、十進数で0.00234375という誤差が発生することになる。
このような計算機特有の誤差を丸め誤差という。
この他に桁落ちというものがある。
例えば、
という計算を考える。
いま仮に10進数で8桁(浮動小数)しか精度を有さない計算機があるとする。
そして、これを使って上の計算を行おうとすると、
最初8桁あった有効精度が5桁に落ちてしまう。
このように、近い数同士の引き算をする場合、計算の精度が落ちてしまうことがある。
このような現象を桁落ちという。
しかし、次のように計算すると、
と精度が保たれる。
今のコンピュータ、とりわけ電卓は賢いので、どのように計算しても同じ計算結果を出すが・・・。
わかりやすいように10進数を使って説明しているけれど、正確な議論をする場合、コンピュータは2進数で計算をしているので、2進数を使って議論をしなければならない。
この点は留意して欲しい。
この他に、たとえば、十進数で3桁しか精度を持たないコンピュータの場合、1000+1を計算すると、
となってしまう。
このように、大きな数(?)と小さな数(?)の足し算でも情報が落ちる情報落ちという現象が起きる。
整数3桁しか扱えないコンピュータなどあるものかと思うかもしれないけれど、かつて存在した8ビットのパソコンで扱える整数は、特別な処理を施さないかぎり、±の符合を有する整数の場合−128〜+127、符合を有さない整数の場合0〜255だ。
という計算をするためには、符号なしの整数の場合、最低でも10ビット必要でそれほど荒唐無稽な話ではないのである。
上の有効精度3桁というのは極端な例だが、Fortranで1000000+0.001を単精度で計算させると、次のような計算結果が得られる。
0.001という情報が落ちてしまっている。
つまり、情報落ちが発生している。
また、先に話したように、0.001は、一旦、2進数に変換されるので、これを10進数に戻すときに1.00000005×10⁻³となっており、丸め誤差が発生していることもわかると思う。
このように、コンピュータで計算する場合、打ち切り誤差以外の様々な誤差が計算に混入する。そして、時に、計算途中で誤差が誤差を次々と生み出し、それが雪だるま式に膨れ上がり、この誤差の蓄積のために、とんでもない計算結果が得られるのであった。