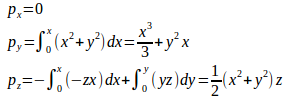第３１回 ソレノイド的なベクトル場

第３１回　ソレノイド的なベクトル場

ある領域で恒等的にdiv A=∇・A=0となるベクトル場を回転的、またはソレノイド的（管状、湧き出しなし）であるという。

領域Dで連続なベクトル場Aが他のベクトル場pによって

　A=rot p=∇×p

とあらわされるとき、Aはベクトルポテンシャルをもつといい、pをAのベクトルポテンシャルという。

A=∇×pのとき、∇・A=∇・(∇×p)=0になるので、ベクトルポテンシャルをもつベクトル場はソレノイド的になる。

単連結領域において、A=∇×p₁=∇×p₂とあらわさせるとする。このとき、恒等的に∇×(p₁−p₂)=0が成り立つので、前回の定理よりp₁−p₂はスカラーポテンシャルφをもち、p₁−p₂=∇φとなる。

つまり、pがベクトル場Aの一つのベクトルポテンシャルであるとき、p+∇φもベクトルポテンシャルになる。

A=∇×pとすると、∇×(∇φ)=0だから、

　　∇×(p+∇φ)=∇×p+∇×(∇φ)=∇×p=A

となるので、p+∇φもAのベクトルポテンシャルになっている。

では、単連結領域において非回転的であるとき、つまり、∇×A=0であるときスカラーポテンシャルφが存在するように、回転的なとき、つまり、∇・A=0のときベクトルポテンシャルpは存在するのかという問いに答えるのが、次の定理。

定理　全空間において連続な偏導関数をもつベクトル場Aがソレノイド的であるとき、A=rot p=∇×pとなるベクトルポテンシャルが存在する。

【証明】

任意の１点(x₀,y₀,z₀)を選びベクトルポテンシャルを次のように定義する。

　　

この回転を計算すると、∇・p=0だから

　　

となる。

同様に、

　　

となる。したがって、このpはAのベクトルポテンシャルである。

（証明終）

上の証明は何を書いているからわからないと思う。

　　

は

　　

という連立偏微分方程式の解の一つ。

として、②と③を解くと

　　

で、これを①に代入すると

　　

となって、④より

　　

だから、

　　

で、φ=0とすると

　　

となり、
　　

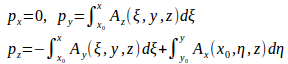
となる。

問題　ベクトル場A=xyi−zxj+(x²+y²)kが回転的であることを示し、かつ、そのベクトルポテンシャルを求めよ。

【解】
　　

よって、回転的である。

混乱しないと思うから、ξをx、ηをxとするけれど、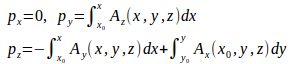
　　

を、x₀=0として使うにゃ。

　　

タグ：ベクトル解析