第４２回 直交軸とベクトル２

第４２回　直交軸とベクトル２

直交軸の変換によって直角座標は次のように変換される。

　　

だから、

　　

となり、

　　

となる。

また、

　　

だから、

　　

となる。

 

ということで、問題。

問題１　をスカラー関数とすれば、

　　

はベクトルである。

【解】

のの座標における値をとすれば、だから

　　

となる。

（２）より

　　

だから、

　　

となり、

　　

はベクトルである。

ちなみに、問題１はスカラー関数の勾配だケロ。

問題２　をベクトル場とするとき、

　　

はスカラーである。

【解】

　　

で、

　　

よって、

　　

だから、

　　

で、

　　

なるので、

　　

となり、値は変わらない。つまり、スカラーである。

このことは、ベクトルの発散は座標軸のとり方によって値は変わらない、ということを言っている。

何を書いているかわからないだろう。わからないのが普通だから、今は気に病むことはないケロ。

これはもうベクトルを越えてテンソルに入っているんだからわからなくて当たり前。
オレはこの記事の式を作っている時に、どこまで式を作っているかわからなくなり、パニクったにゃ。

これでベクトル解析は終わりです。

お疲れ様でした。

タグ：ベクトル解析

第４１回 直交軸の変換とベクトル

第４１回　直交軸の変換とベクトル

直交軸の変換

　　

によって直交座標は

　　

に変換される。

点Aを始点、点Bを終点とするベクトルをvとする。さらに、A,Bの座標をとすれば、直交軸の変換によっては次のように変換される。

　　

よって、

　　

になる。

x¹、x²、x³軸とx’¹、x’²、x’³軸に対するvの成分をそれぞれとすれば

　　

となり、

　　

によって、ベクトルvの成分は次のように変換される。

　　

この（４）が（３）による直交軸の変換によるベクトルの成分の変換式ということになる。

ということで、新たなベクトルの定義を提示。

順序のある３つの数の組v¹、v²、v³があるとする。直交座標の変換

　　

によって

　　

のように変換されるとき、この３つの数の組をベクトルといい、のおのおのをベクトルの成分という。

これに対して、直交座標の変換によって値が変わらないものをスカラーまたは不変量という。

をベクトルとするとき、で与えられる３つの数の組はベクトルになる。

はベクトルなので、

　　

になり、

　　

となる。

そして、とおけば、

　　

になるので、はベクトルということになる。

また、φをスカラーとするとき、もベクトルになる。

、とする。

　　

となるので、はベクトルである。

問題１　２つのベクトルをとすれば、

　　

はスカラーである。

【解】

　　

よって

　　

で、

　　

となるので、

　　

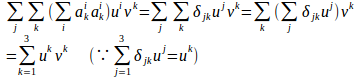
第４０回で出てきたクロネッカーのデルタが大活躍している。ちなみに、クロネッカーのデルタとは

　　

の値をもつ９個の数の組のこと。

この問題の言わんとしていることは、直交座標の変換によってベクトルの内積は不変であるということ。

問題２　ベクトルがスカラー変数tの関数であるとき、

　　

がベクトルであることを証明せよ。

【解】

　　

この両辺をtで微分すれば、

　　

よって、ベクトルである。

タグ：ベクトル解析

番外編 一次変換の回転と軸の回転

番外編　一次変換の回転と軸の回転

高校時代に一次変換や行列を習った人ならば知っていると思うけれど、ねこ騙し数学は、そもそも、数学が苦手な文系の人を対象として始めたので、一次変換の回転について説明するにゃ。

ｘｙ平面に点P(x,y)があり、これを原点を中心にして角度θ（反時計回り）に回転させ、P'(x',y')になったとする。このとき、行列で書くと

　　

という関係がある。

行列の計算法を知らな人もいるでしょうから、普通の計算式で書くと、次のようになる。

　　

この式を導くことは難しくない。

基本単位ベクトルe₁、e₂の回転後の像をe’₁、e’₂とすると、下の図のようになる。

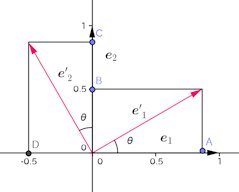
幾何学関係から、

　　

になるので、一次変換は

　　

になる。

何故ならば、回転をあらわす行列をAとすると

　　

よって、

　　

だから。

でだ、

　　

の成分は、e’₁、e’₂のx軸、y軸の方向余弦になっている。

で、x軸（x¹軸）、y軸（x²軸）を反時計回りにθだけ回転した作った新たな座標軸x’¹軸、x’²軸を考える。

この時

　　

だから、新たに設けた座標軸x’¹軸、x’²軸での点Pの成分x’¹、x’²は

　　

となる。

このことは、下の図を見てもらうと分かるでしょう。

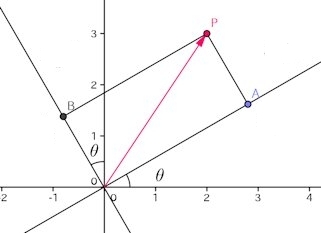
新たな座標軸でのPの成分、x’¹は線分OAで、x’²の成分はOB。
一次変換の回転は、xy平面上の点Pを原点の周りにθ回転させて得られた点P’。

対して、回転による座標軸の変換は、点Pを固定して座標軸そのものをθだけ回転させる。

混同しないように。

タグ：ベクトル解析

第４０回 クロネッカーのデルタ

第４０回　クロネッカーのデルタ

i、jがそれぞれ１、２、３の値をとるとき、９個の数を

　　

を定義したものをクロネッカーのデルタという。

つまり、

　　

である。
で、このクロネッカーのデルタを使うと

　　

になる。同様に、

　　

となる。

だから、

　　

になる。

また、同様に

　　

が成立する。

クロネッカーのδの表記法は

　　

もある。

ということで、問題だにゃ。

問題　直交軸の変換公式

　　

の係数に対して

　　

であることを証明せよ。

【解】

基本単位ベクトルe₁、e₂、e₃は互いに垂直で大きさが１なので

　　

だから、

　　

である。

で、x’¹、x’²、x’³に対するの成分（方向余弦）は

　　

だから

　　

となる。

よって、

　　

となる。

で、

　　

だから、

　　

また、

　　

だから、

　　

（証明終）

なお、

　　

はとても重要な性質です。

タグ：ベクトル解析

数学のソフトで微分積分の問題を解く

数学のソフトで微分積分の問題を解く

数学のお絵描きソフトを新たにゲットしたのを記念して、簡単な微分積分の問題を解いてみることにする。

問題

　　

（１）f(x)=0の解を求めよ。

（２）f(x)の導関数f'(x)を求めよ。

（３）x=−2におけるf(x)の接線を求めよ。

（４）y=f(x)の概形をかけ。

（５）x軸とy=f(x)の囲む領域の面積を求めよ。

（６）f(x)とf'(x)の囲む領域（黄色の部分）の面積を求めよ。

この答は、すべて、ネムネコが持っている数学計算用のソフトで求めることができるんだケロよ。

【解】

（１）　f(x)=x³−3x−2=(x+1)²(x−2)=0

　　　∴ x=−1,2

（２）　f'(x)=3x²−3

（３）　x=aの接線の方程式は

　　

になるので、

　　

（４）　極値をもつためにはf'(x)=0にならないといけない。だから、f'(x)=3x²−3=3(x−1)(x+1)=0。

で、増減表を書くと

x	…	-1	…	1	…
f'(x)	+	0	−	0	+
y=f(x)	増加	極大 0	減少	極小 -4	増加

ということで、概形は次のようになる。

接線と導関数も合わせて書いてあるにゃ。

（４）

　　

x軸とy=f(x)の上下関係はx軸が上でy=f(x)が下なので−が必要だケロ。

（５）　f(x)とf'(x)の交点を求める。

　　

ということで、求める面積は

　　

最後の計算は、数学計算のとあるソフトを使って6√3−9を求めており、ネムネコは、この部分だけは、計算しておりません。

こうした問題は、数学計算用のソフトで簡単に解けてしまう。便利な時代になったよね、ホント。

タグ：微分積分

第３９回 直交軸の変換

第３９回　直交軸の変換

ここで、直交軸の変換として扱う対象は、原点を変えない、右手系の直交軸から右手系の直交軸への変換とする。

また、直交座標を表すのに、x、y、zのかわりに、x¹、x²、x³を用い、基本ベクトルの表記は、これまで使ってきたi、j、kではなく、e₁、e₂、e₃を用いる。ベクトルvの成分はではなく、v₁、v₂、v₃であらわすことにする。

（注意）x、e、vの上下についている数字１、２、３を指標という。x¹、x²、x³は、xの１乗、２乗、３乗の意味ではないので、注意！！

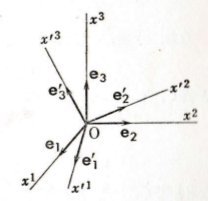
直交軸Ox¹、Ox²、Ox³を他の直交軸Ox’¹、Ox’²、Ox’³に変える場合を考える。

このとき、x¹軸、x²軸、x³軸に対する基本ベクトルをe₁、e₂、e₃とし、x’¹軸、x’²軸、x’³軸に対する基本ベクトルをe’₁、e’₂、e’₃とする。さらに、点Pのx¹軸、x²軸、x³軸に対する座標をx¹、x²、x³とし、x’¹軸、x’²軸、x’³軸に対する座標をx’¹、x’²、x’³とする。x¹軸、x²軸、x³軸に対するx’¹軸、x’²軸、x’³軸の方向余弦、つまり、e’₁、e’₂、e’₃の方向余弦は、それぞれ次のようになる。

　　

逆に、x’¹軸、x’²軸、x’³軸に対するx¹軸、x²軸、x³軸の方向余弦、つまり、e₁、e₂、e₃の方向余弦は

　　

となる。

上と下の指標が逆になっているので注意が必要。

ということで、

　　

また、

　　

となる。

なのだけれど、実は（１）から（２）を、（２）から（１）を直接導くことができる。やってみるにゃ。

　　

で、e’₁のx¹軸、x²軸、x³軸に対する方向余弦をl₁、m₁、n₁と書くことにする。そうすると、

　　

よって、

　　

だから、

　　

となり、

　　

同様に、

　　

となる。

以降、（１）と（２）のように、いちいち、成分に分けて書くのは面倒なので、

　　

とまとめて書くことにする。

さらに、直交軸が（１）のように変換されるとき、点の座標の変化を調べることにする。

点Pのx¹軸、x²軸、x³軸に対する座標をx¹、x²、x³、また、x’¹軸、x²軸、x’³軸に対する座標をx’¹、x’²、x’³とする。

　　

もう一度言うけれど、x¹、x²、x³はxの１乗、２乗、３乗の意味ではない！！

（３）式から

　　

また、

　　

だから、

　　

つまり、

　　

となる。

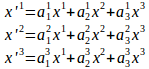
iやjという指標のローマ字には特に意味はないので、（４）のiとjを入れ替えて、

　　

とする。

　――このあたりは融通無碍というか、首尾一貫していないと言おうか――

なのですが、⑨よりは行列を使った方がわかりやすいだろうから、行列を使って書くと、

　　

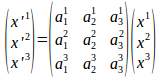
となる。

これからだいたい推測がつくだろうけれど、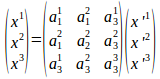

　　

となる。

そして、

　　

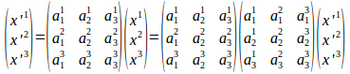
が成立するので、

　　

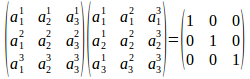
になるのであった。

同様に、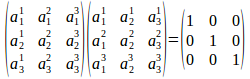
　　

になるのであった。

タグ：ベクトル解析

第３８回 これまでのやり残し

第３８回　これまでのやり残し

前回、球座標（３次元の極座標）のh₁、h₂、h₃を計算することなく、h₁=1、h₂=r、h₃=rsinθとなることを使ったので、まずは、このことから取り上げることにします。

球座標の場合は、u=r、v=θ、w=φになることに注意する。そして、直交座標と球座標には次の関係がある。

　　

ということで、あとは、ただの偏微分の計算になる。

　　

さらに、

　　

そして、

　　

となる。

この計算では、三角関数の

　　

を使っている。

また、

ベクトルAのu、v、wの成分と直交軸に関するには次の関係がある。

これを使って、次の問題を解くことにする。

問題　速度および加速度の円柱座標に関する成分は次のようになることを示せ。

　　

ただし、tについての微分を

　　

とあらわすことにする。
【解】

円柱座標だから

　　

円柱座標のh₁、h₂、h₃はh₁=1、h₂=r、h₃=1。

zについては、そのままだから、計算を改めてする必要はない。

　　

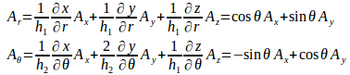
になる。

　　

になるので、

　　

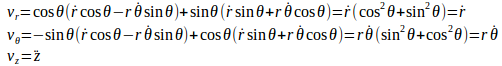
でだ、

　　

を真面目に計算し、この結果を

　　

に代入し、真面目に計算すれば、

　　

になる。

読者のみんながお金を出しあって一万円もお賽銭してくれれば、真面目に計算をしてもいいけれど、でなければ絶対に嫌です。

ちなみに、

　　

なので、注意してほしいニャ。

タグ：ベクトル解析

第３７回 円柱座標、極座標の勾配、発散、回転

第３７回　円柱座標、極座標の勾配、発散、回転

前回、直交曲線座標の勾配、発散、回転を求めた。その結果は以下の通り。

勾配

　　

発散

　　

ラプラシアン

　　

回転

　　

　　

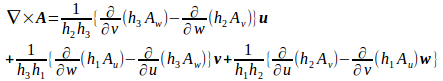
ここで、h₁、h₂、h₃は

　　

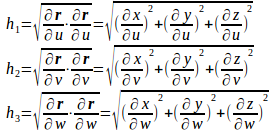
ということで、よく使われる円柱座標、球（面）座標、すなわち、３次元の極座標の勾配、発散などの表示を求めることにする。

円柱座標の場合

円柱座標とは、以下のようなもの。

　　

円柱座標のh₁、h₂、h₃は第３４回の問題１で求めた。その結果は、h₁=1、h₂=r、h₃=1。

だから、円柱座標での勾配は

　　

成分で書くと、

　　

になる。

発散は、

　　

ラプラシアンは

　　

回転は

　　

３次元の極座標（球座標）の場合

３次元の極座標は次のようなもの。

　　

そして、このときh₁=1、h₂=r、h₃=rsinθになる。

勾配

　　

発散

　　

ラプラシアン

　　

回転

　　

タグ：ベクトル解析

第３６回 直交曲線座標における勾配、発散、回転

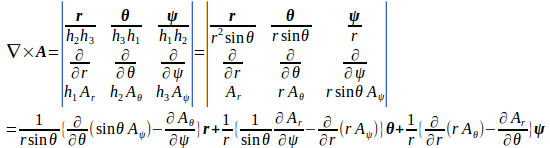
第３６回　直交曲線座標における勾配、発散、回転

勾配

u、v、wの関数をφ(u,v,w)とする。このとき、φの発散は次のようになる。

　　

u=u(x,y,z)、v=v(x,y,z)、w=w(x,y,z)であるとすると、合成関数の偏微分の公式より
　　

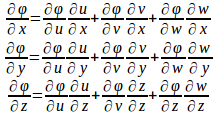
この結果を①に代入して整理すると、

　　

になる。

また、

　　

という関係があるので、
　　

となる。

発散

A(u,v,w)のu成分、v成分、w成分をそれぞれとすると、

　　

となる。

ゆえに、

　　

で、上の式の第１項に注目するのだけれど、ベクトルの微分には次のような公式がある。

　　∇・(φa)=∇φ・a+φ∇・a

また、u=v×w=(h₂∇v)×(h₃∇w)=h₂h₃∇v×∇wだから

　　

で、さらに上の式の右辺第１項は
　　

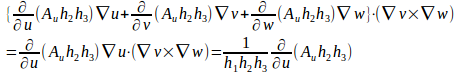
右辺第２項は

　　

ゆえに

　　

についても同様に

　　

となる。

よって、

　　

となる。

さらにA=∇φのとき

　　

なので、
　　

となる。

回転

　　

だから、

　　

右辺第１項は

　　

∇×(∇u)=0だから
　　

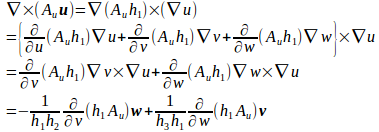
同様に

　　

よって、

　　

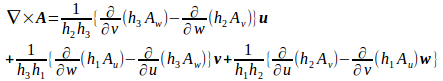
ということで、

　　

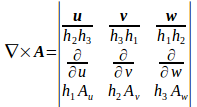
となる。

以上のことより、結果をまとめると、
勾配
　　
発散
　　
ラプラシアン
　　
回転
　　
　　

タグ：ベクトル解析

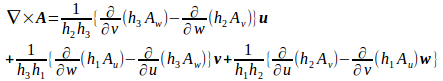
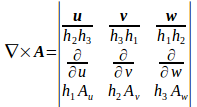
第３５回 曲線座標の続き２

第３５回　曲線座標の続き２

曲面S上の点rは２変数uとvを用いて

　　r=r(u,v)=(x(u,v),y(u,v),z(u,v))

とあらわすことができる。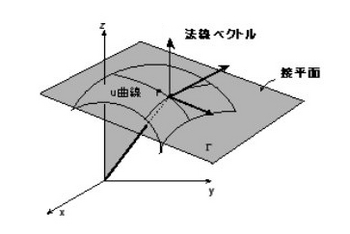

そして、vを固定しuだけを変化させれば曲面S上で一つの曲線を描き、これをu曲線という。同様にuを固定しvだけを変化させればv曲線が得られる。

また、
　　
はそれぞれu曲線の接線ベクトル、v曲線の接線ベクトルである。

u、vをそれぞれu曲線、v曲線の単位接線ベクトルは

　　

となる。そして、この曲面Sの単位法線ベクトルwは

　　

uとvが直交する時は|u×v|は辺の長さが１の正方形の面積で1になるから

　　w=u×v

になる。

u曲線、v曲線に直交し、こうして得られたwと向きが同じ曲線をw曲線とする。
第３３回でやったけれど、u、v、wが直交するとき、線元素は
　　

ただし

　　

となるという話をした。

上の式を見ればわかるけれど、

　　

だから、

　　

また、

　　

はw曲線の接線ベクトルであり

　　

となる。

さらに、ベクトル解析の番外編で述べたグロスマン記号なるものを使うと、

　　

で、[uvw]は辺の長さ１の立方体の体積だから１だにゃ。

つまり、

　　

になるにゃ。

また、３３回で

　　

になるということをやったにゃ。

だから、

　　

で、[uvw]=1だから

　　

そして、さらに

　　

という関係が得られる。

問題　u=h₂h₃∇v×∇w、v=h₃h₁∇w×∇u、w=h₁h₂∇u×∇vであることを示せ。

【解】

　　

同様に、v=h₃h₁∇w×∇u、w=h₁h₂∇u×∇vとなる。

なにか書かないといけないから、書いただけだにゃ。

でも、こちらの方が第３３回のu曲線、v曲線、w曲線の話よりはわかりやすいんじゃないか。３３回で書いたu曲線、v曲線、w曲線の話は何を書いてあるのか、非常に分かりづらいから。

 

タグ：ベクトル解析