ニュートン法

ニュートン法

f(x)を微分可能な関数とする。

方程式

　　

の解をx=αとする。

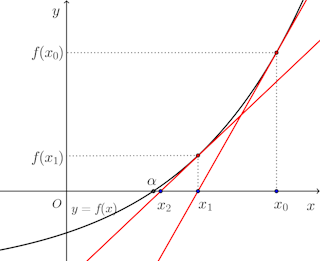
右の図のように適当な点x₁を選び、y=f(x)の点(x₁,y₁)における接線の方程式は

　　

で、この接線とx軸との交点のx座標x₂は、上の式にy=0を代入することによって、

　　

となる。

そして、同様ににおける接線の接線を引き、この接線とx軸との交点のx座標x₃を求めると、

　　

となり、この操作を繰り返せば繰り返すほど、こうして求められたf(x)=0の近似値であるは

f(x)=0の解、x=αに近づいてゆくことが予想される。

これがニュートン法である。

漸化式の形で書けば、ニュートン法は次のようになる。

　　

x=√3の近似値をニュートン法を用いて求めることにする。

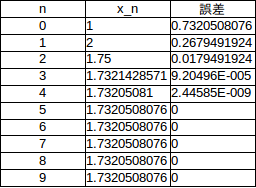
x=√3の両辺を２乗すると

　　

これを

　　

とおき、f(x)=x²−3=0（x>0)とすれば、これはx=√3と同値。

f'(x)=2xだから、

　　

計算開始のx₀=1として、表計算ソフトを使って計算したものは次の通り。

４、５回計算するだけで、x=√3≒1.732050808という近似値に到達している。

ニュートン法は前回の２分法よりも速く、しかも急速に収束することがわかると思う。

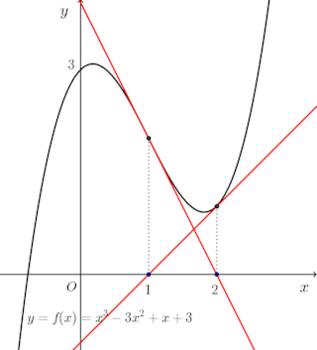
ただし、ニュートン法は、次の例のように、収束しないことがある。

　　

計算の初期値としてx₀=1、または、x₀=2を取ると、

接線の方程式が、それぞれ、

　　

となり、x=1とx=2を交互に永遠に行き来する。

この他にも、f'(x)=0になる点に差し掛かったとき、ゼロ割が発生するなど、危険な一面も有している。

こういうことは極まれにしか起きないけれど、運悪くこのような事態に遭遇することがある。

２分法と比較すると、ニュートン法は収束の速度は速いけれど、安定性に欠ける。

タグ：微分積分 数値解析