第８回 無限級数５

第８回　無限級数５

問題１

数列について、であり、すべてのnに対して、のときは、この数列は収束する。

この定理は使っていいものとして、次の問いに答えよ。

（１）　rは一定の数で、0<r<1とする。すべてのnに対してが成り立つとき、無限級数
　　
は収束することを示せ。

（２）　n²>n(n−1)であることをつかって、次の級数が収束することを示せ。

　　

【解】

（１）　だから、

よって、とおくと、

　　

また、0<r<1だから

　　

よって、

　　

は単調増加で、すべてのnに対してだから収束する。

（２）　n²>n(n−1)だから、n≧2に対して

　　

したがって、
　　　　

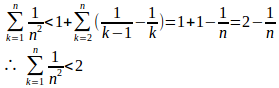
とおくと、1/n²>0だから、数列は単調増加数列で、かつ、すべてのnに対してだから、この無限級数は収束する。

（解答終了）

 

問題２　級数は収束する。このことを使って、級数が収束することを示せ。

また、級数との和をそれぞれS、Tとするとき、SとTの間の関係式を求めよ。

【解】
　　

とおく。

　　

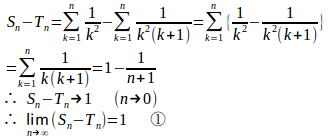
数列とは収束するので、①より

　　

となり、は収束する。

したがって、

　　

である。

【解】

①から、

　　

としてはいけない。

とが収束することTに収束することがわかっていないから。

問題１の

数列について、であり、すべてのnに対して、のときは、この数列は収束する。

という定理を使っていいのならば、次のように証明することもできる。

すべての正の整数kについてk²(k+1)>k²だから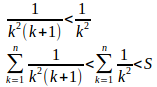
　　

また、だからは単調増加で、すべてのnに対してだから、上記の定理より収束する

なお、問題１の（２）は積分を使うと、次のように証明できる。

k≧2とする。

x∈[k−1,k]のとき

　　

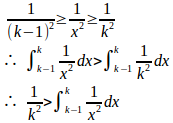
よって、

　　

この両辺に１を加えると、

　　

・・・

 

問題３　次の条件を満たす数列は収束するか。

【解】

（１）

　　

（２）

　　

よって、
　　

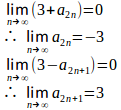
よって、は収束しない、振動する。

（解答終了）