第８回 チェビシェフの不等式と大数の法則

第８回　チェビシェフの不等式と大数の法則

チェビシェフの定理（チェビシェフの不等式）

確率変数Xの平均、標準偏差をそれぞれm、σであるとすると、次の不等式が成り立つ。

　　

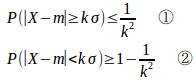
ただし、kは任意の正の数とする。

これをチェビシェフの不等式という。

【証明】

確率変数Xの値がであるときの確率をそれぞれとすると、

　　

そこで、に属するグループと、にわけると
　　

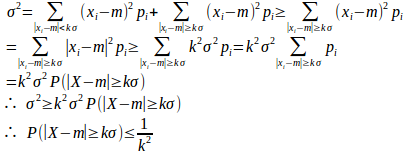
そして、

　　

（証明終了）

ベルヌーイの大数の法則

１回の試行において事象Aの起こる確率をpとし、n回の試行において事象Aの起こった回数をrとすると、任意の正数εに対して

　　

である。

【証明】

Aの起こる確率分布は２項分布だから、平均、標準偏差は

　　

チェビシェフの不等式

　　

に代入すると、

　　

それで、

　　

よって、

　　

εは任意の正数だから

　　

とおくことができ、

　　

したがって、

　　

p.q、εは正の定数だから

　　

したがって、

　　

である。

（証明終了）

問

「n個の値の算術平均（相加平均）をmとし、標準偏差をsとするとき、これらのn個の内の不等式

　　

は

　　

よりも多い」

という定理を用い、ある学級の生徒数は２８０人で、その平均点は６２点、標準偏差は４点であるという情報だけから５４点と７０点の何人より多く、また、５０点と７４点の間にあるものは何人より多いか判断せよ。

【解】

54≦x≦70のとき、m=62、s=4だからk=2。

したがって、

　　

よって、２１０人より多い。

50≦x≦74のとき、k=3だから

　　

したがって、２４８人より多い。

（解答終了）

得点を確率変数Xとする。Xの分布が正規分布に従っているとすると、

　　

とおくと、Zは標準正規分布N(0,1)に従う。

　　

だから、

　　

したがって、54≦x≦74の区間にいる生徒数は

　　

となり、約２６７人になる。

同様の計算をすると、50点と７４点の区間にいる生徒数は２７９人となり、ほぼ全員、この区間に収まることになる。

ちなみに、７０点は偏差値７０、７４点は偏差値８０である。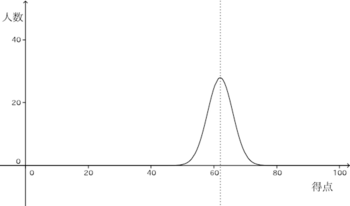

タグ：統計