第３回 広義積分の収束判定法

第３回　広義積分の収束判定法

広義積分の収束判定に関する定理を幾つか紹介することにする。

定理１

関数fを半開区間(a,b]（あるいは[a,b)）で連続とする。が収束するための必要十分条件は、任意の正数εに対して正数δが存在が存在し、a<p<q<a+δ（またはb−δ<p<q<b）に対して

　　

が成り立つことである。

定理２（比較判定法）

関数f(x)、g(x)は(a,b]で不定積分をもち、

　　

であるとする。

このとき広義積分が収束すれば、広義積分も収束する。

区間[a,b)、[a,∞)、(−∞,b]についても同様である。

【証明】

a<t<bとする。
　　

とすると、広義積分が収束するので、

　　

であり、は収束する。

したがって、定理１より任意のε>0に対して、あるδ>0が存在して
　　

よって、

　　

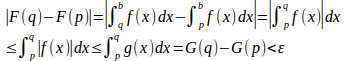
となり、、つまり、広義積分は収束する。

[a,b)、[a,∞)、(−∞,b]についても同様である。

（証明終了）

このような関数g(x)を優関数という。

蛇足ながら、条件｜f(x)｜≦g(x)（a<x≦b）より、a<x≦bにおいてg(x)≧0だから

　　

となり、

　　

である。

定理３

関数f(x)が(a,b]で不定積分をもち、広義積分が収束すれば広義積分も収束する。

[a,b)、[a,∞)、(−∞,b]についても同様である。

【略証】

広義積分は収束するので、任意のε>0に対して、あるδが存在し、

　　　

よって、

　　

[a,b)、[a,∞)、(−∞,b]の証明についても同様。

（略証終了）

 

問１　広義積分

　　

が絶対収束することを示せ。

【解】

x≧0のとき

　　

である。

また、
　　

は、t>0とすると

　　

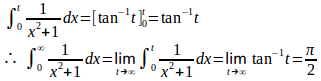
となり、広義積分は収束する。

したがって、定理２より広義積分は収束し、広義積分は絶対収束する。

（解答終了）

 

問２　広義積分

　　

が収束することを示せ。

【解】
　　

と考える。

右辺第１項は[0,1]においてが連続なので通常の積分なので存在する。したがって、右辺第２項の広義積分

　　

の収束判定をすればよい。

x≧1のとき

　　

α=3/2>1だから補題より広義積分は収束する。

したがって、定理２より
　　

は収束する。

よって、広義積分

　　

は収束する。

（解答終了）

問３　広義積分

　　

が条件収束することを示せ。

【解】

　　

と分けて考えることにする。

右辺第１項の

　　

については、(0,π/2]で

　　

であり、

　　

とおけば、定理２より広義積分

　　

は収束する。

したがって、広義積分

　　

が収束することを示せばよい。

そこで、π/2<tとすると

　　

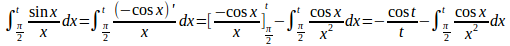
ここで、

　　

また、

　　

であり、
　　

と収束するので、定理２より広義積分

　　

も収束する。

したがって、広義積分
　　

は収束する。

（解答終了）

タグ：微分積分 広義積分