第16回 第15回の問題の別解 [ネコ騙し数学]
第15回の解答とは違う解答を紹介することにする。
問題1
【解】
t=π/2−xとおくと、x=0のときt=π/2、x=π/2のときt=0、また、dx=−dtだから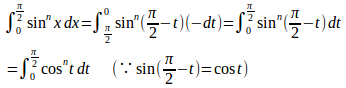
よって
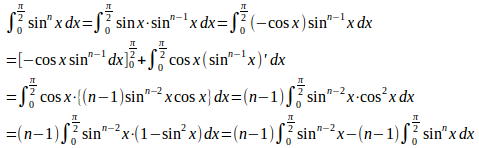
ここで、
nが偶数のとき
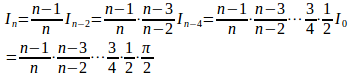
nが奇数のとき
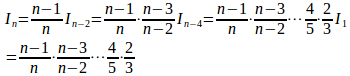
である。
(解答終了)
問題2 次の等式が成立することを証明せよ。
ベータ関数の三角関数表示は
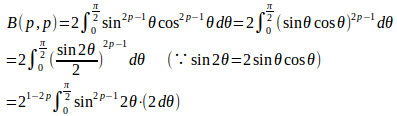
2θ=tとおくと、θ=0のときt=0、θ=π/2のときt=π、またdt=2dθだから
このとき、t=π/2のときs=π/2、t=πのときs=0、またdt=−dsだから
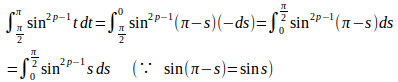
したがって、
したがって
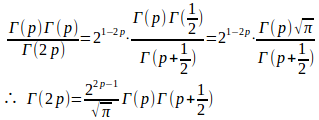
(証明終)
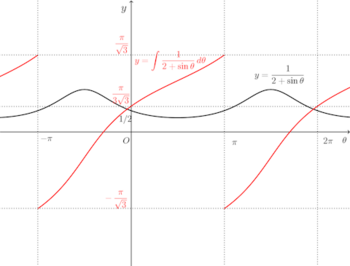
また、
(右図参照)
第15回 ベータ関数、ガンマ関数の問題2 [ネコ騙し数学]
第15回 ベータ関数、ガンマ関数の問題2
問題1
(1)
(2)
ただし、
(3)
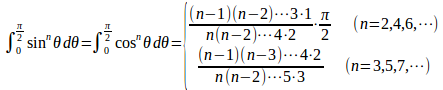
【解】
(1) p=1/2、q=1/2として代入すると
(2)
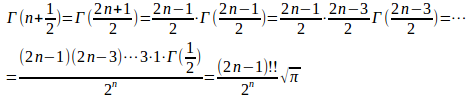
(3) ベータ関数の三角関数表示は
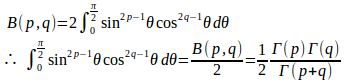
nが偶数のとき、n=2m(m=1,2,・・・)とおくと
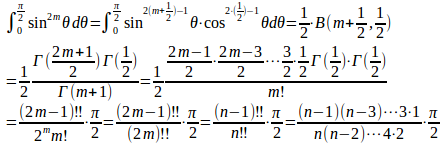
n=3,5,・・・のとき、n=2m+1(m=1,2,・・・)とおくと
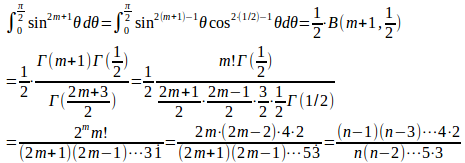
(解答終了)
問題2 次の問いに答えよ。
(1) 次の等式が成り立つことを示せ。
(1)
(2) t=4x(1−x)とおくと、x=0のときt=0、x=1/2のときt=1。
という条件を満たすのは
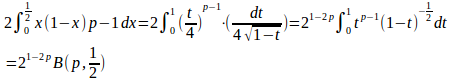
(3)
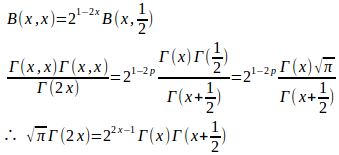
(解答終了)
平均値の定理の問題の続き [ネコ騙し数学]
平均値の定理の問題の続き
問題 fはC²級の関数とする。
f’’(x)≠0ならば
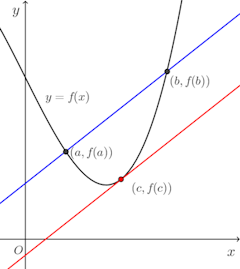
この問題を解く前に、
拡張された平均値の定理
f(x)が閉区間[a,b]でC¹級で、開区間(a,b)で2回微分可能であるとき
【証明】
F(x)は、F(a)=F(b)=f(b)で、[a,b]で連続、(a,b)で微分可能だから、ロールの定理より
(証明終)
ちなみに、
b−a=hとおき、
これで問題を解く準備が整った。
問題 fはC²級の関数とする。
f’’(x)≠0ならば
【証明】
f'(x)に平均値の定理を用いると
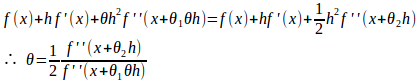
f(x)はC²級、つまり、f’’(x)は連続だから
第14回 広義積分の問題2 [ネコ騙し数学]
第14回 広義積分の問題2
問題1 次の広義積分の値を求めよ。
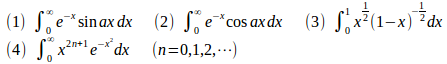
【解】
(1) 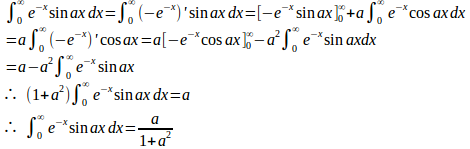
(2)
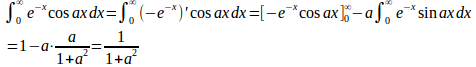
(3) x=sin²θ(0≦θ≦π/2)とおくと
よって、
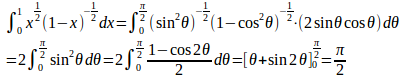
(4) t=x²とおくと
よって、
ベータ関数、ガンマ関数を用いると(3)と(4)は次のように解くことができる。
【別解】
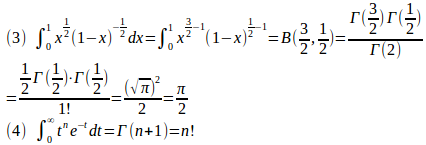
(解答終了)
問題2 f(x)が[0,∞)で連続であるとき、次のことを示せ。
(1) f(x)が有界であるならば、は絶対収束する。
(2) f(x)が非負かつ単調減少でが収束するならば、
である。
【解】
(1) f(x)は有界だから、[0,∞)において
したがって、[0,∞)において
(2) と仮定すると、[0,∞)においてf(x)≧c。
となり、は発散する。
が収束することと矛盾するので、
である。
無限級数の場合、が収束するならば
は成立するが、
広義積分の場合、が収束するならば
という命題は必ずしも成立しないので注意。
今日のアニソン、「ささみさん@がんばらない」から『浸透圧シンフォニー』 [ネムネコ備忘録]
広義積分と複素積分を使って定積分の値を求める [ネコ騙し数学]
まず、
ここで、
u=θ−2πとして、右辺第2項の積分を置換積分すると、θ=πのときu=−π、θ=2πのときu=0、さらに、dθ=duとなるので、
ということで、ε>0として
不定積分を用いてこの定積分の値を求めようとすると、広義積分になってしまう。
【別解】
微分積分の範囲で解けてしまったね。
また、複素関数の積分と留数定理を使うと、次のように求めることができる。
【別解2】
とすると、これはガウス平面(複素平面)の単位円|z|=1となり、さらに
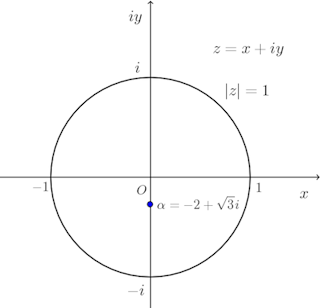
(別解2終了)
定積分の値は求められましたか? [ネコ騙し数学]
問題 次の積分の値を求めよ。
ヒントは、下のグラフです。
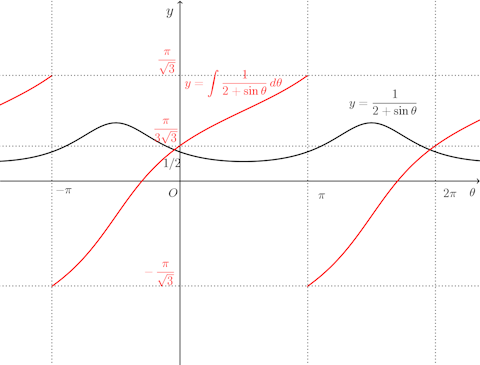
この積分の答えは、
2π/√3≒3.627598728
だにゃ。
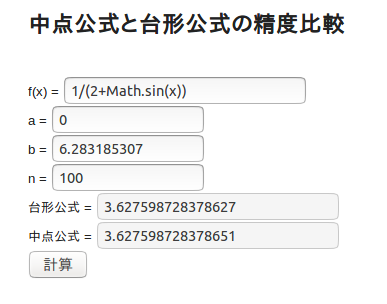
の値とも一致しているので、間違いはなさそうだ。
次の不定積分は
とおくと
これで、不定積分は求まった。
この結果を使って何も考えずに機械的に問題の定積分を計算すると、
へっ、へっ、へっ、へっ。
安易な公式至上主義打倒だにゃ!!
この計算のどこがおかしいか、わかるケロか。
なお、
このように計算してはいけないことのヒントは上のグラフにあるにゃ。
さらに、次の曲を♪
上記の内容は、ネムネコの数学専門ブログ「ねこ騙し数学」にある煽り記事2つを、「ねむねこ幻想郷」用に編集し、一部改変したものです。
平均値の定理の問題 [ネコ騙し数学]
平均値の定理の問題
関数f(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能ならば
平均値の定理Ⅱ
関数f(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能ならば
b−a=hと置けば、平均値の定理は
問題1 f(x)=√x、a=1、b=9のとき、平均値の定理
【解】
この問題の場合、
問題2 のとき、平均値の定理
【解】
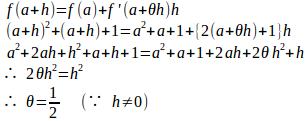
(解答終了)
θ=1/2だから、問題2も点aと点a+hの中点になっている。
θ=1/2という数字には何か秘密がありそうな・・・。問題3 f(x)=x³のとき、等式
となるθについて、を求めよ。
ここでも、θ=1/2という数字が出てきた。
問題4 f(x)は連続な第2次導関数f''(x)を持つ関数で、とする。
【解】
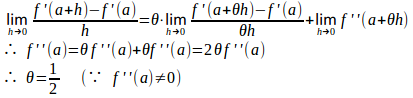
(解答終了)
これは、もはや、偶然とは呼べないだろう。
実は、
関数f(x)がC²級数で、f''(x)=0ならば、
「たしかに愛(i)はあるにゃ、途中で出てくるにゃ」 [ネコ騙し数学]
「ねむねこ幻想郷」の皆さんにお尋ねしますが、
次の積分の値を求められますか?
――できるとは思っていない(^^ゞ――
問題 次の積分の値を求めよ。
この(定)積分の値が存在することは、閉区間[0,2π]で
が連続であることより疑いようがない。
したがって、
「確かに愛(i、i²=−1)はある」にゃ。
数学の公式集や、運良く持っている数学の本にこの一般形の公式が出ているかもしれないけれど、
どんな手段を使ってもいいから、この積分の値を求めて欲しいにゃ。
解析的に解けない人は、シンプソン法や台形公式を使ってこの定積分の近似値を求めてもいいにゃ。
――これだって立派な解法だ!!――
ちなみに、Bloggerにおいてある数値積分のスクリプトによると、この計算結果は次の通り。
(上のものはイメージです。計算ボタンをクリックしても計算はしてくれない)
このスクリプトで計算したい物好きは、
http://nemneko.blogspot.jp/2016/11/blog-post_14.html
ただ、この2つの曲を紹介したかっただけです(^^)
第13回 ラプラス変換入門2 微分方程式への応用 [ネコ騙し数学]
第13回 ラプラス変換入門2 微分方程式への応用
§1 ラプラス逆変換
ラプラス変換の微分方程式の応用について述べる前に、まず、その前提になるラプラス逆変換の定義をあらためて提示し、ラプラス逆変換の簡単な問題を解くことにする。
関数f(t)のラプラス変換
であるとき、ラプラス逆変換は
例えば、
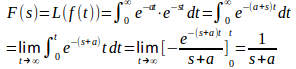
したがって、
上では、積分することでラプラス変換を求めているけれど、この計算をすることなく、前回紹介したラプラス変換表を利用してもよい。
下の表を見れば

問 次のラプラス逆変換を求めよ。
(1) これは
(2) まず
そして、
ここでは、
このばあい、a=−1、a=−−2であることに注意!!
(3)
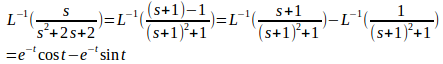
ここでは、a=1、ω=1として
(解答終了)
§2 ラプラス変換の微分方程式へ応用
y=f(t)を[0,∞)上の級とする。そして、この導関数y'=f'(t)のラプラス変換を考えることにする。
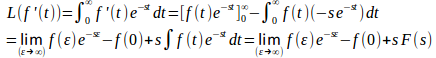
そして、次の極限が
に収束するとき、導関数f'(t)のラプラス変換は次のようになる。
定理(導関数のラプラス変換)
[0,∞)上の級関数f(t)がある2つの定数a、M>0に対して
【証明】
R>0とする。条件より
2次導関数f''(t)については、
以上の結果をまとめると、
問2 ラプラス変換を用いて、次の微分方程式を解け。
L(y)=Yとおくと、
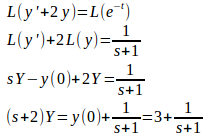
s+2で両辺を割ると
ラプラス逆変換すると、
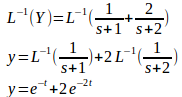
(解答終了)
なお、上の計算では、ラプラス変換表の
もっとも、ラプラス変換表を見るまでもなく
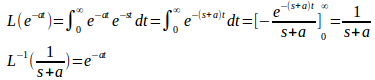
と簡単に求めることができる。
ラプラス(逆)変換を用いれば、面倒な積分の計算をせずに、ラプラス変換表と代数的な演算で微分方程式の解を求めることができる。
問3 次の微分方程式の解を求めよ。
L(y)=Yとおくと
微分方程式の両辺をラプラス変換すると、
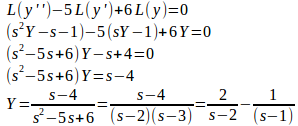
ラプラス逆変換すると、
(解答終了)
ラプラス変換を用いると、積分の計算をせずに、微分方程式を解けるという話。