第２０回 三角形の２辺の和と差

第２０回　三角形の２辺の和と差

定理

三角形において

（１）　２辺の和は第３辺よりも大きい。

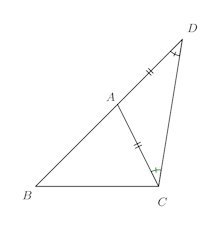
（２）　２辺の差は第３辺よりも小さい。

【証明】
（１）　BAの延長上にAC=ADとなる点Dをとる。

　　BA+AD=AB+AC=BD　　①

三角形ACDはAC=AD、
二等辺三角形だから

　　∠BDC＝∠ACD

よって、

　　∠D=∠ACD<∠BCA+∠ACD∠BCD

第１９回の定理Aより

　　BD>BC　　②

①と②より

　　AB+AC>BC

よって、
三角形の２辺の長さの和は、残りの他の１辺の長さよりも大きい

（証明終わり）

（２）

　　

②より、b−c<a、③よりc−b<a。

よって、

　　

同様に、

　　

（証明終わり）

中学・高校で習ったこの大定理が証明されたにゃ。

問題１　

４角形ABCDにおいて、AB、CDの中点をそれぞれE、Fとすれば、

　　

であることを証明せよ。

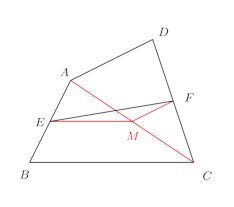
【解】
点AとEを直線で結び、その中点をMとする。

中点連結定理より

　　

（１）　E、M、Fが同一線上にないとき、定理から

　　

（２）　E、M、Fが同一直線上にあるとき、

　　

よって、

　　

（証明終わり）

 

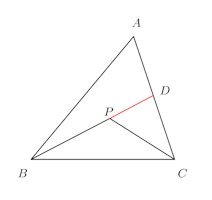
問題２　
△ABC内の任意の１点をPとすれば

　　AB+AC>PB+PC

であることを証明せよ。

【解】

BPの延長とACの交点をDとする。

△ABDに注目すると

　　

△PCDに注目すると

　　

①と②の辺々を足すと

　　

（証明終わり）

問題３　

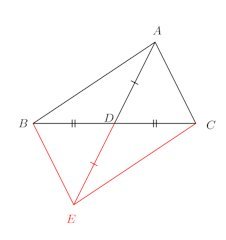
△ABCにおいて、辺BCの中点をDとするとき、次のことを証明せよ。

（１）　AB+AC>2AD

（２）　AB>ACならば∠BAD<∠CAD

【証明】

（１）　ADを２倍に延長したものをAEとする。

対角線をそれぞれが２等分するので、四角形ABECは平行四辺形。

よって、BE=AC

△ABEに注目。

（２）　より∠CAD=∠BEA（錯角相等）。

また、BE=ACだからAB>BE

△ABEに注目。

AB>BEだから

　　

（証明終わり）

 

タグ：初等幾何