第22回 円の性質 [ネコ騙し数学]
第22回 円の性質
§1 円の基本性質
(1) 円の定義
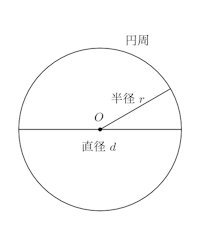
平面上のある1点Oから一定の距離にある点の集合を円という。この点Oを円の中心といい、Oと円周上の点の距離を円の半径という。英語で半径のことをradiusというので記号rであらわす。
直径(diameter)は、円の中心を通り、両端点が円周にある線分の距離のことで、円の直径をdとすると、直径dと半径rの間には
この定義から半径の等しい2つの円は合同になる。
(2) 中心角と弧、弦
円周上に2点A、Bがあるとき、線分ABを弦という。弦を含む直線を割線という。割線によって円は2つの部分に分けられ、分けられたそれぞれを円弧または弧と呼ぶ。
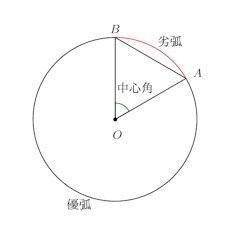
割線によって分割された2つの弧の長さが異なるとき、弧の大きい方を優弧といい、小さい方を劣弧(れっこ)という。また、弧の長さが等しいとき、これらの弧を半円周という。
また、円の弧の両端A、Bと中心Oを結ぶ線分AO、BOのなす角∠AOBを中心角という。
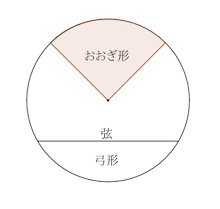
おおぎ形と弓形に関してはもう、図だけで勘弁して。
(3) 中心角と弧、弦についての基本性質
一つの円、または半径の等しい円について
① 等しい弧に対する中心角は等しく、中心角の等しい弧は等しい② 中心角とこれに対する弧は比例する
③ 等しい弧に対する弦は等しく、等しい弧に対する弦は等しいが成り立つにゃ。
これらは直感的にほとんど明らかなので証明しないことにし、円周率πは
(4) 弦の性質
① 中心から弦に引いた垂線は弦の中点を通る
② 弦の垂直二等分線は円の中心を通る③ 中心と弦の中点を通る直線は垂直である
④ 等しい弦は中心から等しい距離にあり、中心から等距離にある弦は等しい図に示すように、中心をOとする円とその円の弦ABがあるとする。
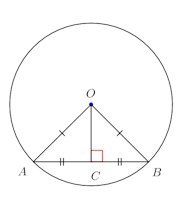
円の定義からOA=OBとなり、△OABはOA=OBとする二等辺三角形になる。
そして、これらは、二等辺三角形の性質からすぐに出てくるケロ。本当ケロか。だんだん面倒くさくさくなって、誤魔化していないか、ネムネコ(^^ゞ
§2 円と直線
(1) 点と直線の距離
点Aと直線lとの距離は、点Aと直線l上の点との最小の距離で、Aから直線lにおろした垂線の長さである。点Aからlにおろした垂線の足をB、点Aと直線lの距離をdとすると、d=ABになるにゃ。
このことは次の図を見れば明らかでしょう。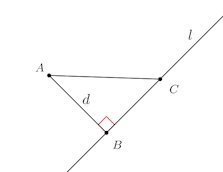
垂線の足であるBと異なる直線上の点をCとし、△ABCを作る。このとき∠ACB<∠ABCだから、AB<ACとなる。だから、点Aと直線lとの距離はABになる。
(2) 円と直線の関係
円の中心をO、半径rの円と直線があり、円の中心と直線の距離をdとする。このとき、円と直線の交点は次のようになる。
① d<r⇔交点が2② d=r⇔交点が1
③ d>r⇔交点が0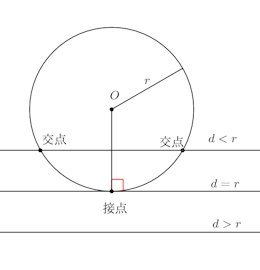
円と直線の交点(共有点)が一つのとき円と直線は接し、その交点を接点という。
定理
円Oの接線は接線を通る半径に垂直である。逆に半径の端における垂線はその点で円に接する。この証明は背理法を使うことになる。
例えば、こんな感じ・・・。「円Oの接線は接線を通る半径に垂直でない」と仮定する。
そして、接点Pとし、円の中心Oから直線lにおろした垂線の足をQとする。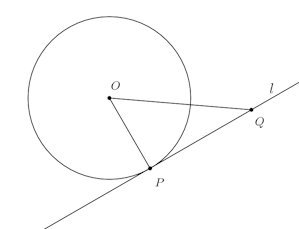
図では∠OQPは90°に見えないけれど、これは90°だにゃ。そう言い聞かせるにゃ。
そして、△OPQに注目。このとき∠OQP=90°だから
∠OQP>∠OPQとなり、角とその対辺の関係から
OP>OQ ①だけど、図から明らかなように
OQ>OP ②でなければならない。何故ならば、OQ<OPであるとすると、Qは円の内部にあることになり、直線と円の交点、共有点が2つになってしまうからだにゃ。つまり、OQ<OPならば、lは接線でないことになってしまう。
で、①と②は矛盾しているので、「円Oの接線は接線を通る半径に垂直でない」とした仮定が間違っているとなる。つまり、円Oの接線は接線を通る半径に垂直である。
こう証明するのならば、①、すなわち、OP>OQならば、Qは円の内部にあることになり直線と円の交点、共有点が2つあることになり、(円の)接線の定義に反する、とした方が素直でしょう。
(円の)接線の定義
円との共有点が1つである直線この接線の定義は円の接線の定義であって、一般の曲線では成立しない。このことは、次の曲線を見れば明らかだにゃ。
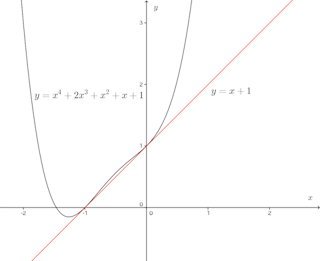
定理
円O外の点Pからこの円に引いた2本の接線の長さは等しい(PA=PB)。また、POは角を2等分し、弦ABを垂直に2等分する。
証明はこの図で十分でしょう。
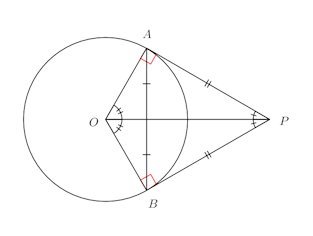
△AOPと△BOPは直角三角形で、AO=BOかつ斜辺OPが共通なので
△AOP≡△BOP
よって、PA=PB
また、合同なのだから∠AOP=∠BOP
∠APO=∠BPOで、POは角を二分するにゃ。
ABの中点をCとするにゃ。OA=OBだから、△OBAは二等辺三角形だから、∠AOBの二等分線はABを2等分するにゃ。
まっ、そういうことで。