関数の連続の復習２ [ネコ騙し数学]
関数の連続の復習２
関数の連続のε-δ論法による定義をあらためて示す。
関数の連続の定義
任意の正数ε>0に対して、あるδ>0があって
であるとき、f(x)は点aで連続であるという。
関数の連続の定義と関数の極限に関する定理（定理１）から次の定理が成り立つことは明らかであろう。
定理４
関数f(x)、g(x)が点aで連続であれば、λ、μを実数とすると、
は点aで連続である。
g(a)≠0ならば
は点aで連続である。
定理５
関数f(x)が点aで連続である必要十分条件は、f(x)が点aで右連続かつ左連続であることである。
［証明］
十分性）
f(x)は点aで連続だから、任意の正数ε>0に対して、あるδ>0があって
よって、
であり、f(x)は点aで右連続である。
また、
だから、f(x)は点aで左連続である。
必要性）
εを任意の正数とすると、f(x)は点aで右連続だからあるδ₁>0があって
で、f(x)は点aで左連続だからあるδ₂>0があって
よって、δ
にとれば
である。
（証明終了）
定理６
関数f(x)が点aで連続かつf(a)≠0ならば、点aの十分近くの点xではf(x)はf(a)と同符号である。
［証明］
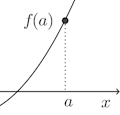f(a)>0の場合を証明すれば十分だから、f(a)>0の場合を証明する。
f(x)は点aで連続だから、任意の正数ε>0に対して、あるδ>0があって
である。
εは任意の正数だから
とおくと、これに対応するδ>0をとれば
（証明終了）
問 f(a)<0の場合の定理６の証明し、証明を完成せよ。
ちなみに、f(a)>0の場合の証明を利用するならば、たとえば、次のように証明すればいいだろう。
f(a)<0のとき、g(x)=–f(x) とおけば、f(x)が点aで連速だから定理４からg(x)も点aで連続でかつg(a)>0になる。
よって、上記の定理６の証明より、点aの十分近くの点でg(x)>–f(x) >0となり、f(x)<0でf(a)<0と同符号になる！！
であるが、ε-δ論法に慣れるために、f(a)>0の場合の上の証明を真似して、自力で証明して欲しい。
ヒントは、
の
を使う。
f(a)<0だから、例えば、
とすればよい！！
