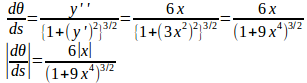曲率と曲率半径 [ネコ騙し数学]
曲率と曲率半径
曲率とは曲線や曲面の曲がり具合をあらわすもので、曲率半径は曲率の逆数である。
問題 半径rの任意の円の微分方程式を作れ。
【解答】
円の中心を(a,b)とすると、半径rの円の方程式は
①の両辺をxで微分すると、
②の両辺をxで微分すると
②と③より
③と④を①に代入して、a、ｂを消去すると
よって、
（解答終）
もし、x=x₀の近傍で曲線y=f(x)を局所的に円に近似できるとすれば、⑤式からこの近似した円（曲率円）の半径（曲率半径）を
求めることができる。
また、②と③式より、円の中心(a,b)は
と求められる。
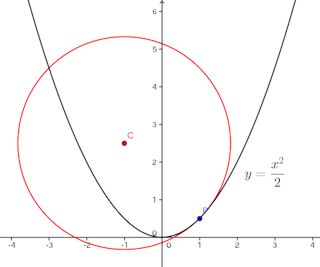
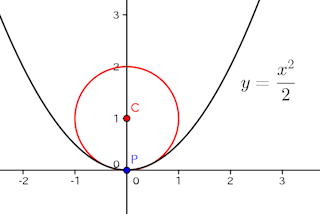
試しに、⑥式を用いて、放物線y=x²/2の点xにおける曲率円の半径を求めてみると、
だから、
よって、x=0のとき曲率半径r=1、x=0のとき曲率半径r=2√2になる。
図を見ると、x=0、ならびに、x=1の近傍の放物線を曲率円が表していることがわかるであろう。
以上のことをまとめると、次のようになる。
曲率円
曲線y=f(x)上の点P(x₀,y₀)において
で定まる円
を曲率円（接触円）という。
さて、一般論。
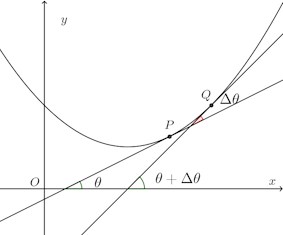曲線上の点P(x,y)における接線とx軸のなす角をθ、曲線上でPに近い点Qにおける接線'がx軸となす角をθ+Δθとし、弧PQの長さをΔsとするとき、
を２点P、Q間の平均曲率といい、
（の絶対値）を曲率、この逆数を曲率半径という。
半径rの円があり、円周上の２点P、Qとこの円の中心のなす角、すなわち中心角をΔθとすると、弧PQの長さΔs=rΔθだから、
となるので、何故、曲率の逆数が曲率半径になるのかが分かるのではないか。
この両辺をxで微分すると、左辺は
だから、
また、
だから、
したがって、曲率と曲率半径κは
である。
点Pにおいて曲線に接し、接線に関して曲線と同じ側にあって、半径が|κ|に等しい円を曲率円といい、その中心)を曲率円の中心という。
問 y=x³の曲率を求めよ。
【解】
したがって、
（解答終了）
