分数関数の微分とそのグラフ

分数関数の微分とそのグラフ

g(x)、h(x)を多項式とするとき、y=g(x)/h(x)の形で表される関数を分数関数、または、有理関数という。

したがって、分数関数の一般形は、n,mを非負の整数とするとき、

　　

分数関数の微分は、商の微分公式

　　

を用いて計算できる。

例

　　

u=x、v=x²+1とおくと、

　　

したがって、f'(x)は
　　

極値をとる点ではf'(x)=0にならなければならないから、

　　

f'(x)の分母は(x²+1)²≧1>0だから、f'(x)の正負は関与せず分子の正負と同じ。したがって、分子の正負の符号だけを調べればよい。

増減表を書くと、

x	・・・	−1	…	1	…
f'(x)	−	0	＋	0	−
f(x)	減少	極小（−1/2）	増加	極大（1/2）	減少

f(x)の２次導関数は、

　　

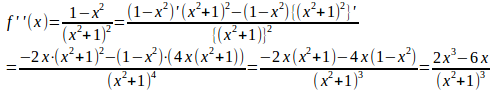
凸凹表は

x	…	−√3	…	0	…	√3	…
f''(x)	−	0	＋	0	−	0	＋
凸凹	上に凸	変曲点	下に凸	変曲点	上に凸	変曲点	下に凸

また、

　　

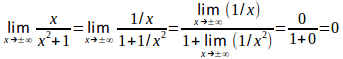
したがって、f(x)のグラフは次のようになる。

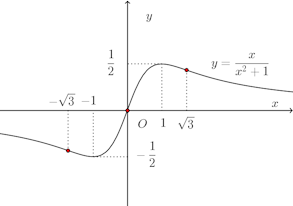
このような簡単な関数ですら、分数関数の微分の計算は大変になるので、２次導関数を用いて極値の判定を行わず、増減表を書いて極値の判定を行ったほうが賢明です。

特に、問題に指示がない場合、変曲点は求めないほうがいい。

分数関数f(x)=g(x)/h(x)とすると、この微分は

　　

極値をとる点をx=αとすると、

　　

したがって、
　　

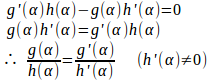
このような関係がある。

例の
　　

の場合、g(x)=x、h(x)=x²+1だから、g'(x)=1、h'(x)=2xだから、極値をとる点をx=αとすると、

　　

になる。

この関数の場合、α=±1であるから、極値の値を上の式を用いて

　　

と計算することができる。

根号などを含む複雑な値の場合、こちらを用いて計算したほうが楽である。

問　次の関数の極値を求め、グラフを書きなさい。

　　

【略解】

（１）

　　

したがって、

極大値　3　(x=−1）

極小値　1/3　（x=1）

（２）

　　

極大値　3　（x=1）

極小値　1/3　（x=−1）

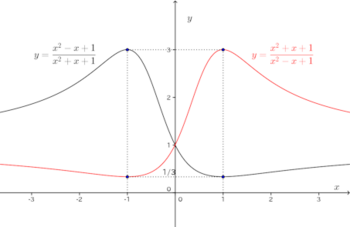
（解答終わり）

（１）の関数をf(x)、（２）の関数をg(x)とすると、g(x)=1/f(x)であるから、実は（２）の極大値、極小値を計算する必要がない。
また、g(x)=f(−x)であるので、g(x)のグラフはy軸に関してf(x)と対称、したがって、g(x)はy(x)をy軸、すなわち、x=0で折り返したものである。

問題　xの関数

　　

は、x=3において極値をとり、x=1における接線の傾きが−2であるようにa、bを定めよ。

【解】

　　

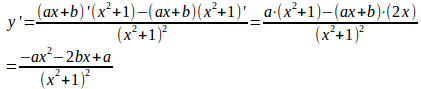
x=3で極値をとるから、x=3のときy'=0でなければならない。

したがって、

　　

また、x=1における接線の傾きが−2だから、x=1のときy'=−2。

したがって、

　　

b=4を①に代入すると、

　　

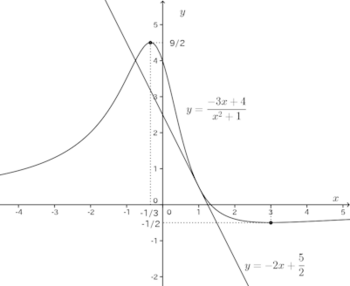
（解答終わり）

問題２　次の関数が極値を持たない条件を求めよ。

　　

ただし、aとbは実数の定数である。

【解】

a=0のとき、f(x)=b/xとなり極値を持たない。

a≠0のときは、

　　

したがって、ax²−b=0が相異なる２実根を持たないことがこの条件。

ax²−b=0の判別式をDとすると、

　　

したがって、ab≦0（註）。

（解答終わり）

（註）　「ab≦0」は、「ab=0」または「ab<0」。「ab=0」は「a=0」または「b=0」だから、「a=0」は「ab≦0」に含まれる。

　　

したがって、b/a>0だと、相異なる２実根を持つ。したがって、極値を持たないためにはb/a≦0でなければならない。

　　

としてもいい。

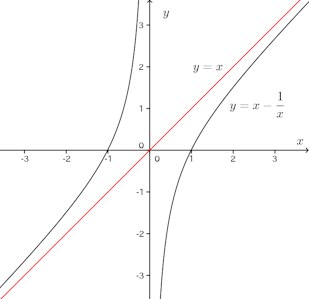
a=1、b=−1の場合を図に示す。

タグ：微分積分