で、お前ら、「１つ質問！！」の答えがわかったのか

で、

お前らは、y=−x²に逆関数があるかどうかわかったんか？

x∈Xからy∈Yへの写像（関数）をf(x)とするとき、y=f(x)に逆関数が存在するためには、XからYへの写像が１対１でなければならない。

しかし、この関数f(x)の定義域は(−∞,+∞)であり、x≠0のとき、f(−x)=f(x)=−x²となって１対１ではないんだケロ。

例　f(−1)=f(1)=−1

したがって、f(x)（−∞<x<＋∞）という関数には逆関数は存在しない。

だけれども、

　　

とすれば、これは１対1の対応になるので、逆関数が定義できる。

この逆関数は、

　　

ここで、一つ、質問。

質問

y=−x²を解くと、

　　

となる。

しかし、

　　

は、この関数の逆関数ではない。

何故だ！！

さらに、なぜ、y≦0になるのか？

 

「なになに、y>0だと、根号の中が負になって、xが虚数になってしまうからだって。やっぱり、逆関数をわかっていないね〜。」

y=−x²のxとyをひっくり返して、

　　

これがこの逆関数だなんてことをやっているヒトにはわからないだろうな〜。

話を逆関数の凹凸に戻すケロ。

これならば、上に凸な関数の逆関数が下に凸な関数になることの反論になっている。

ならない場合がある。

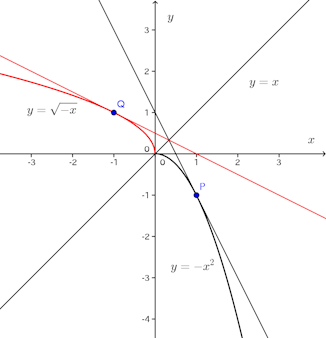
しかし、y=−x²（x≦0）とすると、この逆関数は下に凸になる。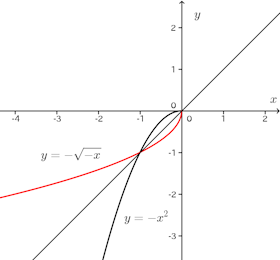

不思議だと思わないケロか？

何かが違うんだケロ。

ヒントは、最初の例だと減少関数、あとの例だと増加関数。

そして、どちらの関数も原点以外で微分可能。

ということは・・・。

思い出せ、逆関数の定義！！




わからないときは、定義に戻って考える。

タグ：微分積分

一つ質問！！ 凸関数の逆関数は凹関数ケロか？

凸関数の逆関数は凹関数？

問　y=√xがある。次の問いに答えよ。

（１）　y=√xの定義域を答えよ。

（２）　y=√xの値域を求めよ。

（３）　y=√xの逆関数を求めよ。

この問題の答えは、

（１）　0≦x（<+∞）

（２）　0≦y（<＋∞）

（３）　x=y²　（0≦y）　あるいは　y=x²　（0≦x）

「（３）の答えを、単に、x=y²、y=x²とするのは致命的な間違い。

何故だろうか？」

「高校のとき、y=f(x)の逆関数はy=xに関して対称と習った。だから、0≦xでなければならない。」

「なるほど、そうですか。だから、y=√xのyとxを入れ換えて、

x=√y

これを２乗すると

x²=y

∴　y=x²

と、y=√xの逆関数を求めるわけですね。」

・・・

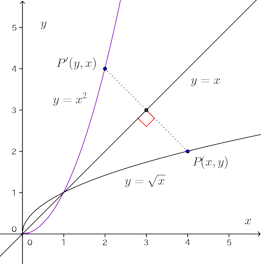
「それはそれとして、この図を見ると、y=√xは上に凸の関数であり、その逆関数であるy=x²（0≦x）は下に凸（上に凹）ですね。同じく、上に凸の関数であるy=logxの逆関数は下に凸な（上に凹な）関数。
したがって、
上にに凸な関数の逆関数は上に凸な関数である。
逆に、下に凸な（上に凹な）関数の逆関数は上に凸な関数である。
これは正しいですか？」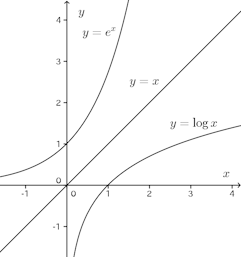

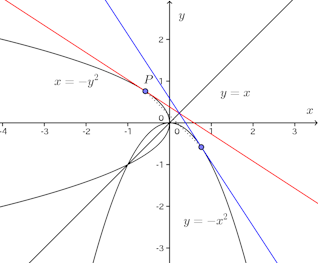
「これは間違い。反例として、次の図をあげる。y=−x²は上に凸であるが、の逆関数x=−y²上の点Pにおける接線は曲線の上にあり、y>0で上に凸。したがって、下に凸（上に凹）になっていない。」

「ほ〜、そうですか。ところで、ひとつ質問しますが、確かに,x=−y²はy=xに関してy=−x²と対称ですけれど、これってy=−x²の逆関数ですか。そもそも、y=−x²に逆関数は存在するんですか？」

へっ、へっ、へっ、へっ。




コイツ、逆関数をまったく理解していない！！
と、⑨³ネコはあざ笑う(^^)

タグ：微分積分

ワンポイントゼミ１１ ニュートン法

ワンポイントゼミ１１　ニュートン法

問題　２次以上の整方程式f(x)=0の実数解の一つをαとする。

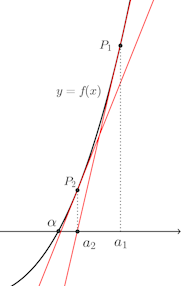
（１）　曲線y=f(x)上のx=a₁に対応する点P₁における接線がx軸と交わる点のx座標をa₂とするとき、次の式が成り立つことを示せ。

　　

（２）　α=a₁+hとおいて、f(a₁+h)の近似式を考えることにより①式で求められるa₂はa₁よりもよい近似値であることを示せ。

（３）　①で求められるa₂に対して

　　

この操作を順次繰り返して方程式の近似値を求める操作をニュートン法という。

①、②を用いて、x³+3x−5=0の近似解を小数点第３位まで求めよ。

【解】

（１）　P₁(a₁,f(a₁))における接線の方程式は

　　

接線とx軸との交点の座標は(a₂,0)だから

　　

（２）　１次の近似式は

　　

f(α)=だから

　　

h=α−a₁だから、

　　

よって、a₂はa₁よりよい近似解である。

（３）　f(x)=x³+3x−5とすると、f'(x)=3x²+3。

a₁=1とすると、f(1)=−1、f'(1)=6だから

　　

a₃の計算は皆さんにお任せします。

a₃≒1.154です。

（解答終わり）

 

タグ：微分積分

関数の近似式

関数の近似式

§１　１次の近似式

関数f(x)がx=aで微分可能ならば、x=aにおける接線

　　

は、x=aのごく近くであれば

　　

という近似ができる。

x−a=hとおくと、x=a+hだから、|h|が十分小さいとき

　　

が成り立ち、①の右辺を１次の近似式という。

特に、①において、a=0、h=xとおけば

　　

例　とすると、

　　

だから、②式より

　　

α=−1、α=1/2とすると、

　　

問　次の近似を求めよ。

　　

【解】

（１）

　　

（２）

　　

 

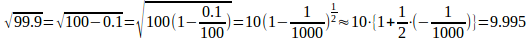
§２　２次の近似式

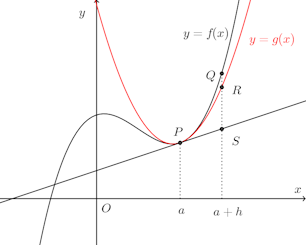
関数f(x)がx=aで２回微分が可能であるとし、点P(a,f(a))で共通の接線を有し、さらに２次微分係数f''(a)が等しい放物線を

　　

とおくと

　　

x=aでf(a)=g(a)、f'(a)=g'(a)、f''(a)=g''(a)であるから

　　

したがって

　　

点Pの近くでは、g(x)はf(x)に近接しているから、x≒aでは

　　

とみなすことが可能で、x=a+hとおけば

　　

という２次の近似式が得られる。

④式から①の誤差がほぼ程度であることが分かる。

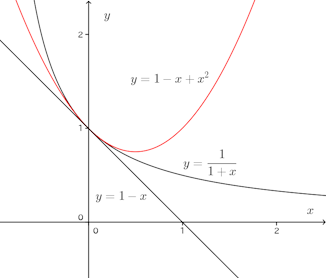
④式においてa=0、x=hととおけば

　　

とすれば、

　　

だから、

　　

α=−1、α=1/2のとき

　　

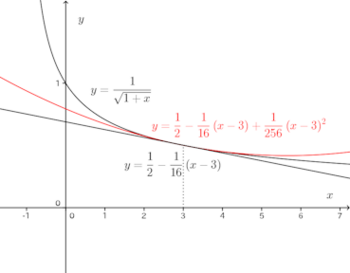
問　xが３に近いとき、次の式の近似式を求めよ。

　　

【解】

　　

とおくと、

　　

ゆえに、
　　

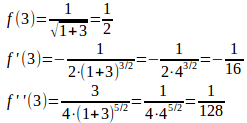
したがって、１次の近似式は

　　

２次の近似式は
　　

タグ：微分積分