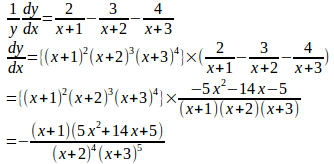微分法を用いた不等式の証明

微分法を用いた不等式の証明

微分法を用いた不等式の証明は、例えば、f(x)>g(x)という不等式の場合、F(x)=f(x)−g(x)とし、微分法を用いてF(x)の増減を調べることが基本。

例　x²>2x−2を証明せよ。

このような問題があった場合、左辺と右辺の差をf(x)と置き、両辺をxで微分する。

　　

よって、x=1のときf(x)は最小（極小）。

したがって、

　　

である、ことが証明できる。

もっとも、この問題の場合、微分を使うまでもなく、

　　

と証明することができる。

では、問題。

問題　x>0のとき、次の不等式が成り立つことを証明せよ。

【解】

（１）

　　

とおく。

　　

したがって、x>0でf(x)は単調増加。

よって、

　　

また、
　　

したがって、g'(x)はx>0で単調増加。

ゆえに、x>0で

　　

よって、g(x)はx>0で単調増加。

　　

①、②より、

　　

（２）

　　

とおく。

　　

よって、f(x)はx>0で単調増加

　　

また、

　　

よって、g(x)はx>0で単調増加。

　　

①と②より、

　　

（解答終わり）
（１）、（２）ともに、マクローリン展開（テーラー展開）を
　　

有限項で撃ち切ったもの。

そして、（２）の
　　

と

　　

から、

　　

という不等式が出てくる。

また、（１）の

　　

の各辺をx=0からx=tまで積分すると、

　　

という不等式が得られる。

図から明らかように、各辺のすべての関数が偶関数なのだから、さらに次の不等式が得られる。

　　

なお、この不等式を得るにあたって、定積分の次の定理を使っている。

定理　f(x)、g(x)が[a,b]で連続、かつ、f(x)≧g(x)であるならば、

　　

f=gは、fとgが同一の関数、つまり、x∈[a,b]のすべてのxに対してf(x)=g(x)である、ことをあらわしている。

宿題　x>0で

　　

であることを利用して、

　　

であることを証明せよ。

タグ：微分積分

対数微分法

対数微分法

非零の値をとる微分可能なxの関数u、vがある。

その積をy=uvとおき、この絶対値
　　

両辺の対数をとると

　　

両辺をxで微分すると
　　

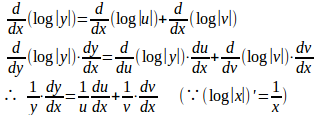
両辺にyをかけると

　　

となり、積の微分の公式が得られる。

また、y=u/vとおき、この両辺の対数をとり、さらにそれを微分すると

　　

と商の微分公式が得られる。

このように、関数の対数をとって、さらに、微分する方法を対数微分法という。

問題１　次の関数を微分せよ。

　　

【解】

両辺の対数をとり、微分すると

　　

（解答終わり）

問題２　次の関数を微分せよ。

　　

【解】

両辺の対数をとり、微分すると、

　　

（解答終わり）

問題３　次の関数を微分せよ。

　　

【解】

両辺の絶対値をとり、さらにその対数をとる。

　　

微分すると、

　　

（解答終わり）

以上のことから、

　　

絶対値をとるのは、対数の真数となるyが負になることがあるから。対数の真数は正の数でないとならない。

なお、

　　

であることは、合成関数の微分を使って次のように示すことができる。

x>0ならば

　　

x<0のとき

　　

だから、

　　

を求めればよい。

そこで、u=−1とおき、合成関数の微分を使う。

　　

x>0、x<0のときでも、

　　

が成立し、したがって

　　

である。

そして、このことから、

　　

という積分公式が得られる。

問題４　次の微分をせよ。

　　

【解】

　　

とおき、両辺の絶対値の対数をとると

　　

両辺をxで微分すると、

　　

（解答）

問題４のように微分する関数が複雑な積の形で与えられているときに対数微分法は有効な計算方法。

タグ：微分積分