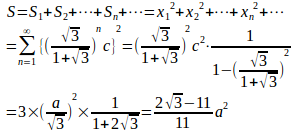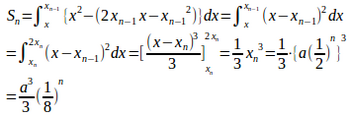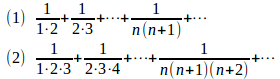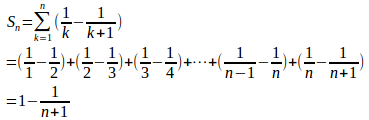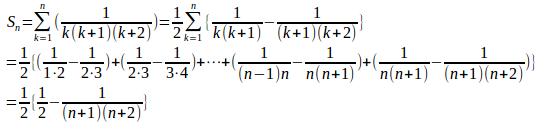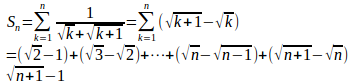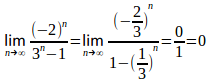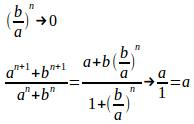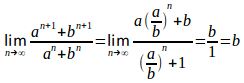第９回 無限級数６ 無限級数の図形への応用 [ネコ騙し数学]
第９回 無限級数６ 無限級数の図形への応用
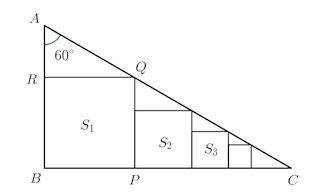
問題１ 右図のように直角三角形ABCの中に正方形S₁、S₂、S₃、・・・が限りなくならんでいるとき、これらの正方形の面積S₁、S₂、S₃、・・・の総和を求めよ。ただし、BC=a、∠A=60°、∠B=90°とする。
【解】正方形S₁、S₂、S₃、・・・の１辺の長さをx₁、x₂、x₃、・・・とし、AB=cとする。
△ABC∽△ARQだから 
（解答終了）
問題２ ２等辺三角形ABCの３辺に内接する円Oの半径をrとする。等辺AB、ACと円Oとに内接する円をO₁とし、AB、ACとO₁とに接する円をO₂とする。このようにして次々と円を作っていくとき、これらすべての円の面積の和を求めよ。ただし∠A=2αとする。
【解】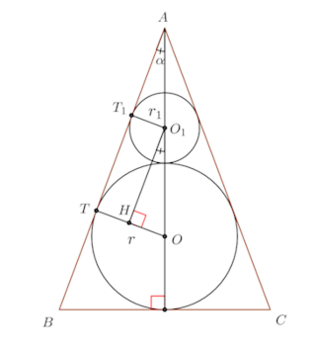
OからAB、O₁からABに下ろした垂線の足をT、T₁、O₁からOTに下ろした垂線の足をHとする。
また、
の面積を
とすると、
は初項
、公比
よって、
問題３ 放物線y=x²をCとする。C上の点A₁(a,b)(a>0）における接線とx軸との交点をP₁とし、P₁を通ってx軸に垂直な直線とCとの交点をA₂、点A₂におけるCの垂線とx軸との交点をP₂とする。以下、同じようにして、C上に
、x軸上に
を作る。
（１） のx座標を、それぞれ
とすると、
はどんな数列になるか。
（２） 図形
の面積を
とするとき、無限級数
を求めよ。
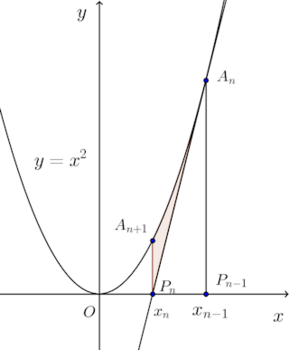【解】（１） dy/dx=2xだから、
における接線の方程式は、 
したがって、は初項a/2、公比1/2の等比数列で、
（２） 図形
の面積は
は初項
、公比1/8の等比数列。
よって、
第８回 無限級数５ [ネコ騙し数学]
第８回 無限級数５
問題１
数列
について、
であり、すべてのnに対して、
のときは、この数列は収束する。
この定理は使っていいものとして、次の問いに答えよ。
（１） rは一定の数で、0<r<1とする。すべてのnに対して
が成り立つとき、無限級数
は収束することを示せ。
（２） n²>n(n−1)であることをつかって、次の級数が収束することを示せ。
（１） だから、
よって、
とおくと、
また、0<r<1だから
は単調増加で、すべてのnに対して
だから収束する。
（２） n²>n(n−1)だから、n≧2に対して
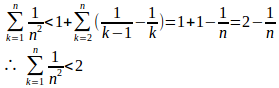
とおくと、1/n²>0だから、数列は単調増加数列で、かつ、すべてのnに対して
だから、この無限級数は収束する。
問題２ 級数
は収束する。このことを使って、級数
が収束することを示せ。
また、級数との和をそれぞれS、Tとするとき、SとTの間の関係式を求めよ。
とおく。
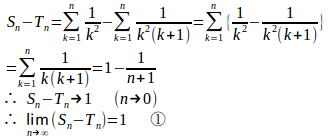
数列
とは収束するので、①より
となり、は収束する。
【解】
①から、
と
が収束することTに収束することがわかっていないから。
問題１の
数列について、であり、すべてのnに対して、のときは、この数列は収束する。
という定理を使っていいのならば、次のように証明することもできる。
すべての正の整数kについてk²(k+1)>k²だから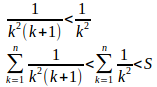
また、
だから
は単調増加で、すべてのnに対して
だから、上記の定理より収束する
なお、問題１の（２）は積分を使うと、次のように証明できる。
k≧2とする。x∈[k−1,k]のとき
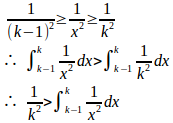
よって、
この両辺に１を加えると、
問題３ 次の条件を満たす数列は収束するか。
【解】
（１） 
（２）
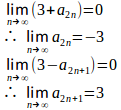
よって、は収束しない、振動する。
第７回 無限級数４ [ネコ騙し数学]
第７回 無限級数４
問題 次の和を求めよ。
x=1のとき
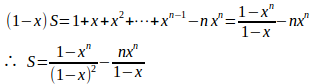
（解答終了）
上で求めた
この証明は、例えば、次のようにすればよい。
【証明】x=0のとき、③は明らか。
0<｜x｜<1のとき 
したがって、
このことから、
問題２
（１） a>0のとき、 
（２） 無限級数
【解】
（１） n≧2のとき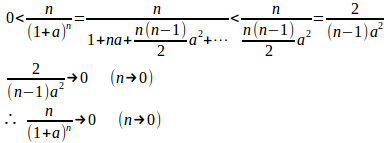 
（２）
②に1/2を掛けると
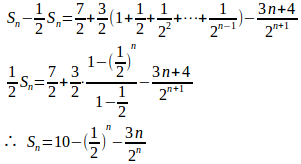
a=1を（１）の結果に代入すると、
問題３ 無限数列が
を満たすとき、次の問いに答えよ。
（２） 次の無限級数の和を求めよ。
（１）
①はn=1のときにも成り立つので、
（２）
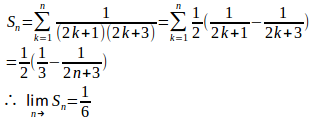
（解答終了）
第６回 無限級数３ [ネコ騙し数学]
第６回 無限級数３
問題１ 次の無限級数の和を求めよ。
【解】
(1) この無限級数の一般項は 
したがって、
（２） この無限級数の一般項は
よって、
問題１を踏まえて、すこしだけ発展した問題を。
問題２ 次の無限級数の和を求めよ。
（１） 一般項は
したがって、部分和は
（２） 一般項は
（３）
問題３ 次の無限級数は発散することを証明せよ。
一般項は
よって、
（解答終了）
第５回 無限級数の和２ [ネコ騙し数学]
第５回 無限級数の和２
問題１ 次の無限等比級数の和を求めよ。
無限等比級数の和の公式を使う。
【解】
（１）は初項a=1、公比
の無限等比級数だから
（２） 公比をrとすると、
よって
（３） 公比rは
よって
問題２ 無限等比級数がある。その和が１で、各項を２乗して作った無限等比級数の和が２である。各項を３乗して作った無限等比級数の和を求めよ。
【解】等比数列の初項をa、公比をrとすると、
問題３ 平面上を動く点Pが、原点Oを出発しx軸の正の方向に1だけ進み、次にy軸の正の方向に2/3だけ進み、次にx軸の負の方向に(2/3)²だけ進み、次にy軸の負の方向に(2/3)³だけ進む。以下、このような運動をかぎりなく続けるとき、点Pの極限の位置の座標を求めよ。
【解】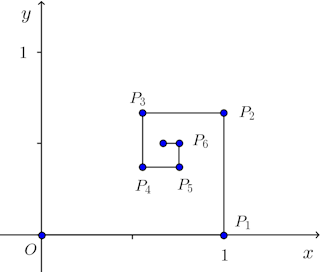
右図のように限りなく進んだ点Pの極限の座標を(x,y)とすると、
原点OをP₀とし、P₀P₁=1とすると、
線分の長さには 
nが1増加すると、進行方向が反時計回りにπ/2=90°変わる。
これ以上書くと混乱を招くだけだから、これ以上は何も言うまい。
第４回 無限級数 [ネコ騙し数学]
第４回 無限級数
§１ 無限級数の収束、発散
無限級数が与えられているとき、
とおくと、数列が得られる。
この数列が収束するとき級数
は収束するといい、収束しないとき発散するという。
そして、が収束するとき、すなわち、
であるとき、この極限値Sを無限級数の和という。
例１
上の無限級数の第n部分和
は
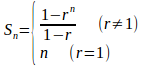
｜r｜<1のとき
だから、このとき数列は
であり、
がこの無限級数の和である。
｜r｜≧1のとき、は収束せず、したがって、発散する。
以上のことから、
無限等比級数 
例２ 無限級数
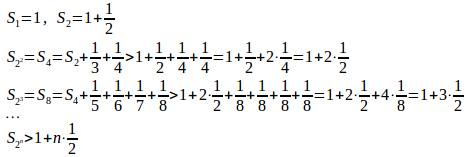
したがって、
よって、
は収束しない。
§２ 無限級数の基本的性質
定理１
とするとき、
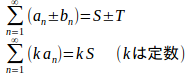
である。
定理２ 無限級数
が収束するためには、
でなければならない。
例２であげた無限級数
したがって、定理２の条件は無限級数が収束するための十分な条件ではなく、必要な条件であることに注意。
問題１ 次の無限級数に和があればそれを求めよ。
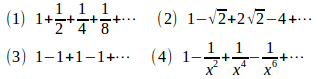
【解】
（１） これは初項a=1、公比r=1/2の無限等比級数。｜r｜=1/2< 1だから式（１）より
（２） 公比r=−√2、｜r｜=√2>1だから収束しない。
（３） 公比r=−1だから収束しない。
（４）
（解答終了）
問題２ 次の無限級数は収束するか。
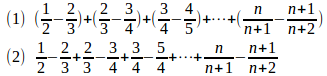
【解】
（１） 第n部分和は
（２）
（解答終了）
第３回 極限の計算２ [ネコ騙し数学]
第３回 極限の計算２
問題１ 次の式を一般項とする数列の極限値を求めよ。
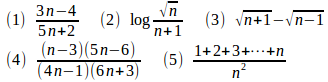
【解】
（１） 分母分子をnで割って 
（２） 分母分子をnで割って
（３） （分子の）有理化をすると
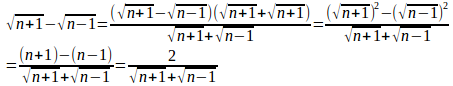
よって、
（４） 分母分子をn²で割ると
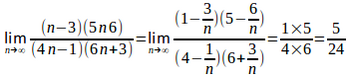
（５）
（解答終了）
問題２ 一般項が次の式で表される数列の収束、発散を論じよ。
【解】
（１） 
（２） 分母分子を
で割ると
、0<1/3<1だから
（３） a=bのとき
（解答終了）
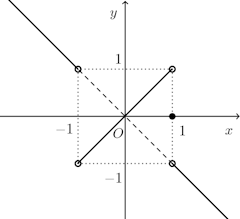
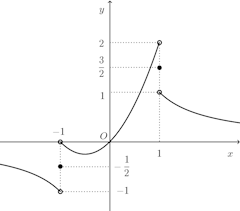
問題３ 次の関数のグラフをかけ。
（１） ｜x｜<1のとき
n→∞のとき
x=−1のとき、f(x)は存在しない。
よって、 
（２） ｜x｜<1のとき
第２回 数列の極限の計算（基本） [ネコ騙し数学]
第２回 数列の極限の計算（基本）
問題を具体的に解くことによって、数列の極限の計算法を学ぶことが今回の目的。
問題１ 次のような一般項を持つ数列の極限を求めよ。
【考え方】
このタイプの極限の計算は、最高次の項をくくりだすとよい。たとえば、（１）のばあいは、
（２）の場合は、分子分母の最高次のn²をくくりだす分母、分子でくくり出すとよい。
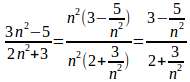
n→∞のとき1/n²→0だから、
より、
【解】
（１）
（２）
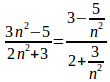
n→∞のとき
（３）
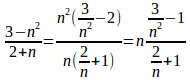
n→∞のとき
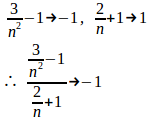
したがって、
（４） 0≦｜cosnx｜≦1だから
問題２ 次の極限値を求めよ。
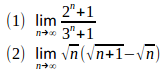
【考え方】
（１） 分母分子で最大の項はだから、これで分母分子を割ると
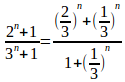
0<2/3<1、0<1/3<1だから、n→∞のとき
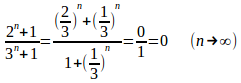
つまり、
（２） これは次のように
の有理化をするとよい。
√nで分母分子を割ると
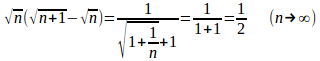
よって、
これをまとめて解答を作ればよい。
今回は基本だけで、次回はより複雑な数列の極限を求めることにする。
計算問題だけでは単調なので、最後に次の問題を解くことにする。
問題３ 数列
が
の関係を満たすとき、次の極限を求めよ。
（１）
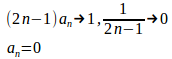
つまり、
（２）
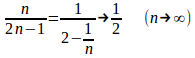
したがって、
（３） （２）より
第１回 数列の極限 [ネコ騙し数学]
第１回 数列の極限
§１ 数列の極限
数列の定義
自然数Nから実数Rへの写像 
を実数列、あるいは数列といい、
あるいは単にと書く。
いまかりに、数列を
を第n項という。がnの数式の形で書かれ、それによって数列が一般的に表されるとき、を一般項という。
例
という数列の一般項は
例で取り上げた数列
は、nが限りなく大きくなると、第n項
は限りなく0に近づく。
このことを「数列の極限値は0である」といい、
一般に、数列において、nが限りなく大きくなるとき、がある一定の数αに限りなく近づくならば、「数列はαに収束する」といい、このことを
と書き、αを数列の極限値という。
問 次の数列の極限値を求めよ。
【答】 （１） 1 （２） 1 （３） 1
数列が収束しないとき、数列は発散するという。
数列が発散するときは、次の３つの場合がある。
（１） が正の無限大に発散する （例 
）
このとき、
と書く。
（２） が負の無限大に発散する （例 
）
このとき、
と書く。
（３） （１）、（２）のいずれでもない場合 （例 
）
（３）の場合を振動するという。
§２ 数列の基本的性質
定理
２つの数列
が収束し、
であるとき
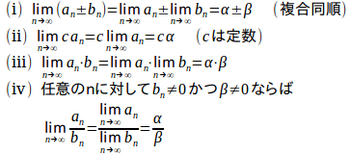
上の定理は、高校の数学の範囲では証明できないので、これは無条件でそのまま受け入れて欲しい。
問題 次の事柄は正しいか。正しくなければ反例をあげよ。
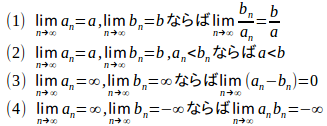
【解】
（１） 正しくない。 
（２） 正しくない。
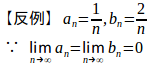
（３） 正しくない。
（４） 正しい。
定理
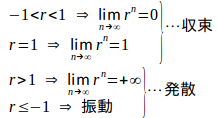
【証明】
（Ⅰ） r>1のときr=1+a（a>0)とおくと、２項定理より
（Ⅱ） r=1のとき
（Ⅲ） r=0のとき
（Ⅳ） −1<r<1のとき
とおくと、b>1だから（Ⅰ）より
（Ⅴ） r<−1のとき
−r=bとおくと、b>1。
nが正の偶数のとき、すなわち、n=2k（kは正の整数）のとき 
（証明終了）
具体的な極限の計算は次回。
