第１７回 ロピタルの定理 [ネコ騙し数学]
第１７回 ロピタルの定理
ロピタルの定理Ⅰ
関数f(x)、g(x)は点aのある近傍で連続、aを除いた近傍で微分可能、かつ、g'(x)≠0とする。このとき、f(a)=g(a)=0であり、
が存在するならば
も存在し、
である。
［証明］
xを点aの近傍の点とする。
x>aのとき、f(x)、g(x)は閉区間[a,x]で連続、開区間(a,x)で微分可能、かつ、g'(t)≠0（t∈(a,x)）だから、コーシーの平均値の定理より
であるcが存在する。
したがって、x→a+0のときc→a+0だから、
である。
x→a–0 のときも同様に
が存在するので、
したがって、
（証明終了）
ロピタルの定理Ⅱ
関数f(x)、g(x)は点aのある近傍で連続、aを除いた近傍で微分可能、かつ、g'(x)≠0とする。このとき、
であり、が存在するならばも存在し、
である。
ロピタルの定理Ⅱのように、ロピタルの定理の条件がf(a)=g(a)=0ではなく、の場合は、
とおき、F(x)、G(x)にロピタルの定理Ⅰを適用すると、
となり、ロピタルの定理Ⅱの証明が証明される。
ロピタルの定理Ⅲ
関数f(x)、g(x)が無限区間(a,∞)で連続で微分可能で、かつ、g'(x)≠0とする。このとき、
であり、
が存在するならば、
も存在して、
である。
［証明］
a>0とする。
t=1/xとおくと、(a,∞)は(0,1/a)に写される。したがって、x→∞はt→0+0になる。
とおくと
となるから、
よって、ロピタルの定理Ⅱより、
が存在して、
したがって、
a<0のときも同様に証明される。
（証明終了）
ロピタルの定理Ⅳ
関数f(x)、g(x)は開区間(a,b)で微分可能でg'(x)≠0とする。このとき、
で、さらに
が存在するならば、
も存在し、
である。
［証明］
とおき、0<ε<1とする。
このとき、δ₁>0が存在して
a<x<c<a+δ₁のとき、[x,c]でコーシーの平均値の定理を用いると、
であるξが少なくともⅠつ存在する。
この式は次のように変形可能。
だからg(x)>0としてよく、
cを固定すると、だから
よって、適当なδ₂>0を選ぶと、
したがって、δ=min(δ₁,δ₂)にとると
よって、
である。
（証明終）
同様に、次のロピタルの定理Ⅴが証明される。
ロピタルの定理Ⅴ
関数f(x)、g(x)は開区間(a,b)で微分可能でg'(x)≠0とする。このとき、
で、さらに
が存在するならば、
も存在し、
である。
そして、ロピタルの定理Ⅳとロピタルの定理Ⅴから、次のロピタルの定理Ⅵが証明される。
ロピタルの定理Ⅳ
関数f(x)、g(x)は点aを除く点aの近傍で微分可能でg'(x)≠0とする。このとき、
で、さらにが存在するならば、も存在し、
である。
凸関数の問題２ [ネコ騙し数学]
凸関数の問題２
問題を解く前に、関数の凹凸の定義を再掲する。
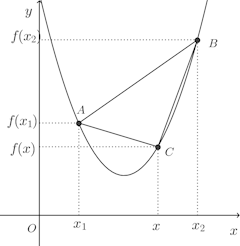区間Iで定義された関数f(x)が、Iの任意の点x₁、x₂（x₁<x₂）に対して、x₁<x<x₂ ならば
であるとき、f(x)を凸関数という。また、このとき、f(x)は下に凸という。
また、 –f(x)が凸関数であるとき、f(x)を凹関数という。
とおくと、（１）式は
と変形できる。
したがって、凸関数の定義に、（１）、（２）式のどちらを使用してもよい。
また、1–t =α、t=βとおくと、（２）式は
となるので、（３）式を凸関数の定義に使用してもよい。
また、f(x)が凸関数のとき、
が成立し、
直線AC勾配≦直線ABの勾配≦直線CBの勾配
である。
さらに、次の定理をあらためて紹介する。
定理 （凸関数と２次導関数）
関数f(x)が区間Iで連続、区間Iの内部で２回微分可能とする。f(x)がIで凸関数である必要十分な条件は、Iの内部でf''(x)>0であることである。
問題１ 次の問に答えよ。
（１） 開区間Iでf(x)>0、f(x)は２回微分可能とする。このとき、logf(x)が凸関数ならばf(x)が凸関数であることを証明せよ。
（２） 区間でf(x)>0とする。logf(x)が凸関数ならばf(x)は凸関数であることを証明せよ。一般に逆は成立しない。
［解］
（１） logf(x)はIで２回微分可能。
問題の条件よりlogf(x)は凸関数だから、定理より
。
よって、
したがって、logf(x)が凸関数であるとき、f(x)は凸関数である。
（２） x、yを区間Iの任意の点とし、0<t<1とする。
logxは増加関数だから、
logf(x)がで凸関数ならばf(x)も凸関数になる。
（解答終）
（※） a>0、b>0、0<t<1のとき
である。
問題２ fは区間Iで定義された凸関数とする。このとき、次のことを証明せよ。
（１） 任意のx∈Iに対して
は増加関数である。
（２） Iが開区間であるとき、fは任意の点x∈Iで右側微分および左側微分が可能である。
（３） Iが開区間であるとき、fは連続である。
［解］
（１） 凸関数の定義より明らか（右上のグラフ参照）。
（２） x₁<x<x₂とする。
xとx₂を固定し、x₁を増加させると、（１）より
は増加する。また、
だからは上に有界である。したがって、x₁→x-0のとき極限値
が存在する。すなわち、
であり、点xで左側微分可能である。
xとx_1を固定しx₂を減少させると、（１）より
は減少し、
だから、は上に有界。したがって、
が存在し、点xで右側微分可能である。
（３） Iが開区間のとき、（２）より、任意のx∈Iでfは右側、左側微分が可能である。したがって、fは点xで左側連続、右側連続。したがって、fは点xで連続である。
（解答終了）
（３）を式で書くと
そして、問題２は次の定理の証明になっている。
定理 関数fが閉区間[a,b]で凸関数ならば、fは開区間(a,b)で連続である。
