第20回 数列の極限とその定理 [ネコ騙し数学]
第20回 数列の極限とその定理
数列
自然数全体の集合をNで表す。すなわち、N={1, 2, 3, ・・・, n, ・・・}。
自然数Nから実数Rへの写像を実数列、または、数列といい、記号
![]() あるいは単に
あるいは単に![]() で表す。これは実数を
で表す。これは実数をと並べたものである。
数列の収束
数列![]() が次の条件を満たすときα∈Rが存在するとき、
が次の条件を満たすときα∈Rが存在するとき、![]() はαに収束するという。
はαに収束するという。
任意のε>0に対して、あるmが存在して、
である。
定理1 (数列の極限の一意性)
【証明】
また、
とすると、ある正の整数m₂があって
よって、m=max{m₁,m₂}とすると、任意のε>0に対して
となり、|α–β|=0となり、α=β。
(証明終)
定理2 (収束数列の有界性)
【証明】
ある1つの値にε>0をとると、ある正の整数mがあって、n>mならば
である。
そこで、
の最大値をMとすると、
よって、収束する数列は有界である。
(証明終)
定理3 (数列の極限の大小)
数列は収束し、
であるならば、
である。
【証明】
任意のとおくと、
より、ある正の整数m₁があって
より、ある正の整数m₂があって
よって、m=max{m₁,m₂}にとると、n>mならば
となり、に矛盾。
ゆえに、α≦βである。
(証明終)
定理4 (数列の極限の公式)
定理5 (ハサミ打ちの定理)
すべての正の整数nについてで、かつ、
ならば、
である。
【証明】
![]() より、任意のε>0に対して、ある正の整数m₁があって、n>m₁ならば
より、任意のε>0に対して、ある正の整数m₁があって、n>m₁ならば
より、任意のε>0に対して、ある正の整数m₂があって、n>m₂ならば
また、だから、m=mas{m₁,m₂}にとると、
よって、である。
(証明終了)
定理6 (有界な単調数列の収束性)
![]() が単調増加数列かつ上に有界(単調減少数列かつ下に有界)ならば
が単調増加数列かつ上に有界(単調減少数列かつ下に有界)ならば![]() は収束する。
は収束する。
【証明】
上に有界な単調増加数列の場合について証明する。
したがって、
で、かつ、任意のε>0に対して
であるmが存在する。
したがって、n>mならば
よって、
下に有界な単調減少数列の場合も同様。
(証明終)
定理7
【証明】
条件より、![]() は上に有界な単調増加数列、
は上に有界な単調増加数列、は下に有界な単調減少数列。よって、定理6より、
![]() は収束する。
は収束する。
とおくと、定理3よりα≦β。
よって
したがって、
【証明終了】
定理8 (区間縮小法)
閉区間の列において
ならば、すべての閉区間に含まれる1点αが存在し、
である。
第0回 方向微分と偏微分、そして、全微分 [ネコ騙し数学]
第0回 方向微分と偏微分、そして、全微分
§1 方向微分と偏微分
fをR²の部分集合DからRへの写像(関数)とし、さらに、u=(h,k)とする。
tを変化させたとき、
の平均変化率は
をとり、t→0の時の(1)式の極限
を考えると、これはベクトルu=(h,k)に沿っての変化率で、u=(h,k)に沿っての方向微分係数という。これを記号で表す。すなわち、
である。
特に、u=e₁=(1,0)としたときの、e₁=(1,0)に沿っての方向微分係数
は、yをbに固定してxだけを変化させたときの変化率であり、関数fの点(a,b)でのxに関する偏微分係数といい、記号、などで表す。それ故、次のように表すことができる。
u=e₂=(0,1)としたときの、e₂=(0,1)に沿っての方向微分係数
は、xをaに固定してyだけを変化させたときの変化率であり、関数fの点(a,b)でのyに関する偏微分係数といい、記号、、
などで表す。同様に、
問1 次の関数の点(0,0)における、xとyの偏微分係数を求めよ。
【解】
(解答終)
1変数関数f(x)は、x=aにおける微分係数f'(a)が存在するならばx=aで連続であるが、2変数関数f(x,y)の場合、点(a,b)の偏微分係数が存在してもf(x,y)が点(a,b)で連続である保証はない。
たとえば、問1の関数f(x,y)は点(0,0)で連続でない。
§2 全微分
関数f(x)が点x=aで微分可能である必要十分条件は、
である。ここで、A=f'(a)であり、o(h)はランダウ記号(ランダウのスモール・オー)、すなわち、
である。
(8)式を2変数関数f(x,y)に拡張すると、
になるであろう。ここで、A、Bはh、kに無関係な定数であり、
である。
この関係式(9)が成り立つとき、2変数関数f(x,y)は点(a,b)で全微分可能、あるいは、微分可能であるという。
f(x,y)が全微分可能であるとき、(9)式より、
![]()
となり、f(x,y)は点(a,b)で連続である。
定理
f(x,y)が点(a,b)で全微分可能ならば、f(x,y)は点(a,b)で連続である。
また、k=0とすると、(9)式は
となり、両辺をhで割りh→0の極限を求めると、
である。
同様に、k=0とすると、
よって、(9)式は
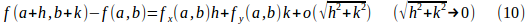
になる。
定理
f(x,y)が点(a,b)で全微分可能ならば、点(a,b)で偏微分可能で、
である。
次に、h、kを定数とし、th、tkを(10)式のh、kと見なすと、(10)式は
となり、両辺をt≠0で割り、t→0の極限をとると、
![]()
これは、u=(h,k)に沿っての方向微分係数であるから、2変数関数f(x,y)が点(a,b)で全微分可能ならば、点(a,b)で任意のu=(h,k)に沿っての方向微分係数をもち、
が成り立つ。
以上のことから、f(x,y)が点(a,b)で(全)微分可能ならば方向微分可能であり偏微分可能である。
リプシッツ連続に関係がありそうな問題 [ネコ騙し数学]
リプシッツ連続に関係がありそうな問題
リプシッツ連続
関数f(x)は区間Iで定義されているとする。このとき、任意のx₁、x₂∈Iに対して、ある実定数K≧0が存在して、
であるとき、f(x)はIでリプシッツ連続という。
リプシッツ連続に関係のありそうな問題を紹介する。
問題1 αを方程式x=f(x)の解とする。関数f(x)が微分可能で、0<|f'(x)|<1であるとき、x₂=f(x₁) (x₁≠α)は、x₁よりも方程式x=f(x)のいい近似解であることを証明せよ。
【解】
平均値の定理より、
であり、
だから、
(解答終)
問題1の条件では、x=f(x)の解はただ一つである。意欲のあるヒトはこの証明にチャレンジするとよい。
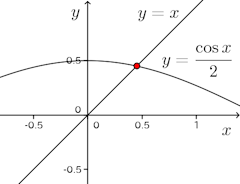 問題1とは、すこし条件が違うけれど、たとえば、
問題1とは、すこし条件が違うけれど、たとえば、という方程式があるとする。
とすると、f(x)は微分可能で、
αを方程式x=f(x)の解とすると、
となり、
と逐次計算することによって、αという収束解を得ることができる。
x₁=0とし、10回ほど反復計算すると、x=0.450184という近似解が得られる。
この計算に使用したC言語のプログラムと計算結果を参考までに紹介することにする。
#include <stdio.h>
#include <math.h>
double f(double x) {
return 0.5*cos(x);
}
main() {
double x1, x2;
int i, n = 10;
x1=0.;
printf("n x1 x2\n");
for (i = 1; i <=n; i++) {
x2 = f(x1);
printf("%d %f %f\n", i , x1, x2);
x1=x2; //計算結果の更新
}
printf("x=%f\n", x2);
}
計算結果
n x1 x2
1 0.000000 0.500000
2 0.500000 0.438791
3 0.438791 0.452633
4 0.452633 0.449649
5 0.449649 0.450300
6 0.450300 0.450158
7 0.450158 0.450189
8 0.450189 0.450182
9 0.450182 0.450184
10 0.450184 0.450184
x=0.450184
問題2 f(x)は微分可能な関数で、任意の実数x,yについて次の関係式を満たしている。
このとき、f(x)を求めよ。
【解】
x≠yとする。
とおくと、
yを固定し、x→yのときのF(x)の極限を求めると、ハサミ打ちの定理より
よって、F'(x)は定数。この定数をCとおくと、
(解答終)
⑨から一気に⑨³を結論してもいいと思うけれど、また、f(x)は微分可能な関数という条件もいらないと思うけれど、念の為に、問題にはつけておいた。
問題3 関数f(x)とその導関数f'(x)は、任意の実数x₁、x₂に対して、次の関係を満たしている。
(1) このとき、
(2) f(x)は1次式で表されるかまたは定数である。
【解】
(1)
任意の実数x₁、x₂に対して問題の不等式は成り立つので、問題の条件の不等式のx₁、x₂を入れ替え
![]()
よって、
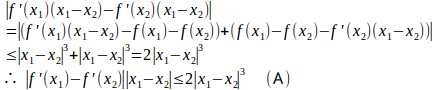
x₁≠x₂のとき、(A)式の両辺を|x₁–x₂|≠0で割り
x₁=x₂のとき
よって、証明された。
(2) x₁≠x₂とする。
任意のx₂に対してf''(x₂)=0だから、f(x)は一次式で表されるか定数である。
(解答終了)
対数微分を用いて・・・ [ネコ騙し数学]
問題 関数の増減を調べることにより、次の不等式を導け。
m、nが3<n<mである整数ならば
関数の増減を調べるためには、
の微分ができなければならない。
この微分を求めるには、x>0、y>0だから、の両辺の対数をとり、それを微分すればよい(対数微分法)。
つまり、
あるいは、
になるので、
と計算することもできる。
なおここで、
であり、
という指数関数の公式を使っている。
微分もできたことなので、問題を解くことにする。
よって、はx=eで極大、かつ、最大である。
2<e<3だから、x>3でyは減少する。
(1) 問題の条件より3<n、また、yはx>3で減少関数だから、
である。
(2) 3<n<mだから
両辺をnm乗すると、
(解答終)
ちなみに、2⁴=4²=16だから、n=2、m=4のとき(※)の不等式は等号が成立する。
問 次の問に答えよ。
(1) 次の極限を求めよ。
(2) (1)の結果を利用して、次の極限を求めよ。
ちなみに、(1)の
の極限を求めるのに、ロピタルの定理は使えない!!
ロピタルの定理を使うと
リプシッツ連続と一様連続 [ネコ騙し数学]
第19回 リプシッツ連続と一様連続
Xを実数Rの空でない部分集合とし、fをXからRへの関数とする。このとき、任意のx₁、x₂∈Xに対して、あるK≧0が存在し、
であるとき、fはXでリプシッツ連続という。また、(1)式の定数Kをリプシッツ定数と呼ぶ。
関数f(x)がXでリプシッツ連続であるとき、f(x)がXで連続であることは、次のように証明できる。
すべてのx₁、x₂∈Xとする。
K=0のとき、(1)式より、
となり、f(x)は定数関数。よって、Xの各点で連続である。
K>0のとき、x₁を固定し、任意の正数に対して、δを
をとれば、
になるので、f(x)はすべてのx₁∈Rで連続である。
また、このことから、関数f(x)がリプシッツ連続であれば一様連続であることがただちにわかる。
一様連続
fを区間Iで定義された関数とする。任意のε>0に対し、次の条件を満たすδ>0が存在するとき、fはIで一様連続であるという。
一様連続の定義から、関数f(x)が区間Iで一様連続であればIで連続であることは明らか。そして、リプシッツ連続であれば一様連続であるので、次のような関係がある。
リプシッツ連続⇒一様連続⇒連続
一般に、逆は成立しない。
一様連続に関しては、重要な次の定理があるが、証明なしで定理だけを紹介しておく。
定理
関数fが有界閉区間Iで連続ならば、fはIで一様連続である。
上のは、有界閉区間でなければ、一般には成立しない。
例1 f(x)=x²(0≦x<∞)は一様連続でない。
とおき、δ=1/nとする。
このとき、
このようなx₁、x₂を取った場合、nを大きくし、δ>0を限りなく小さくして0に近づけても、1より小さくなることはない。よって、f(x)は[0,∞)で一様連続ではない。
(注)
一様連続の定義は
したがって、一様連続でないは、上の否定
例1ではこれを使用している。
これを数学で使われる翻訳調日本語に訳すと、
一様連続でないとは、
あるε>0が存在し、任意のδ>0に対して、あるx₁、x₂∈Iが存在し、
を満たすことである
とか(^^ゞ
また、次のように、区間Iが有界閉区間でなく、有界な開区間であっても、Iで連続な関数な関数がIで一様連続になることがある。
例2 f(x)=x²(x∈(0,1))は区間(0,1)で一様連続である。
任意のx₁、x₂∈(0,1)とする。
したがって、f(x)は(0,1)でリプシッツ連続であり、一様連続である。
あるいは、任意のε>0に対して、δ=ε/2>0をとると、
よって、一様連続である。
次の例3のように、有界な区間でなくても、リプシッツ連続であり、一様連続になる場合もある。
例3 f(x)=sinx (x∈(−∞,∞)) は(−∞,∞)でリプシッツ連続であり、一様連続である。
任意のx₁、x₂∈(−∞、∞)とする。
したがって、sinxは、(−∞,∞)でリプシッツ連続であり、一様連続である。
あるいは、任意のε>0に対して、δ=ε>0をとると、
よって、一様連続である。
問1 平均値の定理を使って、
が成り立つことを証明せよ。
問2 f(x)=logx (x≧1)は[1,∞)で一様連続か。
【解】
x₁、x₂∈[1,∞)とし、x₁≠x₂とすると、平均値の定理より
となるcがx₁とx₂の間になる。
したがって、c>1となり、
よって、任意の正数ε>0に対して、
とδを定めれば、
任意のε>0に対して、
よって、[1,∞)で一様連続である。
(解答終)
余力のあるヒトは、「f(x)=√x (x∈[0,∞))は[0,∞)で一様連続か」にチャレンジしてみるといいだろう。
問題 区間Iで微分可能な関数f(x)が、任意のx、y∈Iに対して
を満たせば、関数f(x)は定数である。
【解】
任意のx、y∈I(x≠y)とする。
したがって、fはIで定数である。
(解答終)
一点で微分可能であるが、それ以外の点で連続でない関数 [ネコ騙し数学]
関数の定義域の一点で微分可能であるが、それ以外の定義域の点すべてで不連続な関数の一例。
このとき、f(x)は、x=0で微分可能で連続であるが、それ以外の点すべてで連続でない。
x=0で微分可能であることは、例えば、次のように証明されるだろう。
x≠0とする。
xが有理数のとき
xが無理数のとき
いずれにせよ、
よって、
x=0でf(x)は微分可能なのだから、f(x)はx=0で連続である。
ε-δ論法がよければ、(1)のところを次のようにすればいいだろう。
任意の正数ε>0に対してδ=ε>0にとれば、
x=0以外で連続でないことを証明するのは、例えば、次のようにすればいいだろう。
a≠0とする。
とすると、どんなδ>0をとっても
であるxが存在する(下図参照)。

何故ならば、δ>0をどんなに小さくしても、aが有理数、xが無理数のとき、
であり、aが無理数、xが有理数のとき
となり、(2)を成立させるxが|x–a |<δに存在するからである。
よって、a=0以外の全ての点でf(x)は連続ではなく、微分不可能である。
(※)
「関数f(x)が点aで連続である」のより正確な定義は、
したがって、点aで連続でないは、(2)を否定した
である。
積分形式のテーラーの定理 [ネコ騙し数学]
積分形式のテーラーの定理
関数f(x)は区間Iで級で、a、b∈Iとする。
このとき、
が成立する。
この式の右辺を部分積分すると、
同様に部分積分すると
したがって、
さらに、同様にこの操作を続けてゆくと、
を導くことができる。
これが、積分形式のテーラーの定理である。
微分形式のテーラーの定理は、
したがって、積分形式と微分形式のテーラーの定理とではラグランジュの剰余項の表現が異なっている。問題は、この2つが同じものかどうかであろう。
積分の第1平均値の定理
関数f(x)、g(x)は閉区間[a,b]で連続、かつ、g(x)≧0とする。このとき、
が成り立つξが少なくとも1つ存在する。
a<bのとき、[a,b]でだから、積分の第1平均値の定理より
となり、剰余項の表現形式が積分形式と微分形式と異なるもので、同一の定理であることが理解してもらえるのではないだろうか。
定理 (積分形式のテーラーの定理)
f(x)が区間Iで級、a∈I、任意のa∈Iに対し、
である。
特に、fがIで級で、任意のx∈Iで
ならば、任意のx∈Iで
である。
微分の問題・・・の続き [ネコ騙し数学]
前回の話の続き!!
前回、関数f''(x)が点aの近傍(a–r,a+r)(r>0) でC²級であれば、
であるということを示した。
では、
と、f(x)の2次微分係数f''(a)を(1)式の右辺で近似したときの誤差はどの程度だろうか?
fが級であるとき、O形式のテーラーの定理は
である。
n=2とすると、
になる。
これを(1)式に代入すると、
だから、(1)の近似式の誤差はh程度と予測できる。
だが、近似式(1)の誤差h程度ではない。このことは、、a=1とし、h=0.1、h=0.01の場合で計算すると、このことはすぐに確かめられる。
実際、h=0.1のときの誤差は0.00226599、h=0.01のときの誤差は0.000022652で約1/100になっている。つまり、hを1/10にすると、誤差は約1/100になっており、誤差はh²に比例していることになる。つまり、(1)式の近似式の誤差はO(h²)である。
なぜ、このようなことが起きたかというと、n=3としてf(a+h)をテーラー展開すると、この理由がわかる。
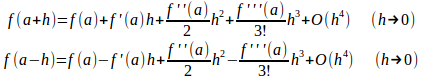
奇数次の項の符号がf(a+h)とf(a–h )では正負が異っており、f(a+h)とf(a–h )を足し合わせると、奇数次の項が消えてしまうのだ。だから、誤差はO(h)ではなく、O(h²)になってしまう。実際、これを(1)式の右辺に代入すると、
となることからも確かめられる。
矛盾しているといえば矛盾していないし、矛盾していないといえば矛盾していないような気がする(^^ゞ
実は、これと同じような奇妙なことが次の極限を求めるときに発生する。
(2)、(3)式から、x→0のとき、sinxは、xと同位の無限小でO(x)で、かつ、O(x³)であるということになる。ランダウの記号、関数の無限小の定義からそうなると言われればそれまでなのだが、考えてみれば、これも奇妙な話のように思えてならない。どうやら、微分積分や解析学、そして、数値計算などでよく使用されるランダウの記号は正体不明の、かなり胡散臭いシロモノ、バケモノなのかもしれない。
何しろ、ランダウ記号(ビッグ・オーO)の計算規則は、
で、普通の算法は通用しないのだから。
したがって、これを使うときには細心の注意が必要に違いない。
さて、ランダウ記号の計算規則⑨が成立する例として、
としたときの誤差を調べてみることにする。
だから、
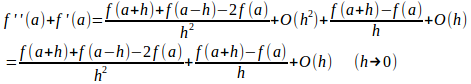
になるはずである。
、a=1として、hを変化させて、絶対誤差
を計算してみると、次のグラフのような結果になる(赤線)。
比較参照のために、
を用いて、f''(a)+f'(a)を計算した値もグラフ中に示してある(緑線)。
グラフの縦軸には近似値との誤差の絶対値を、横軸にはhをとり、対数グラフで計算結果を示してある。
赤の直線(?)の勾配が約1で誤差がh程度、緑の直線の勾配が約2でh²程度であることから、近似式⑨³の誤差がO(h)であること、そして、計算規則⑨の妥当性が確かめられると思う。
関数の極限、微分の問題を膨らませて、すこし、数値解析・・・ [ネコ騙し数学]
題 f(x)=sinxとするとき、次の極限を求めよ。
この問題をただの三角関数の極限と考えれば、三角関数の和積や倍角公式を使って次のように解くことができるだろう。
【解】
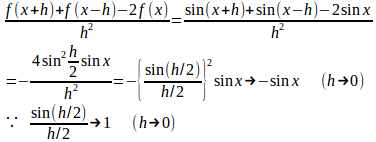
(解答終了)
三角関数の極限と考えれば、これはこれで立派な解答だろう。しかし、それでは、もったいないと思う。
(1)は分母分子がともに0になる0/0の不定形の極限で、f(x)=sinxは何回でも微分可能な関数。したがって、ロピタルの定理を使って、分子分母を2回hで微分すると、次のように解くことができる。
【別解1】
f(x)=sinxは2回微分可能で、(1)は0/0の不定形の極限。ロピタルの定理を使い、分母分子をhで微分すると、
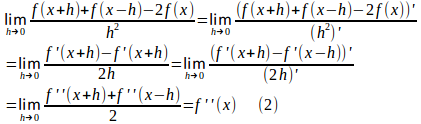
また、
よって、
(解答終)
f(x)が2回微分可能であれば、(2)式から(1)の極限はf''(x)で、(1)はf(x)の2次導関数f''(x)の導関数を与えるということがわかる。
また、o形式のテーラーの定理、
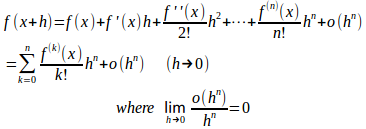
を使うのならば、n=2として、
次のような解答を作ることもできるだろう。
【別解2】
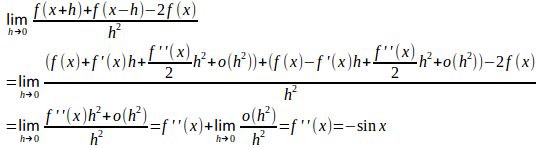
(解答終)
ところで、f(x)が微分可能のとき
である。
そこで、
とx=aにおける微分係数f'(a)を近似したとき、(A1)と(B1)の近似式のほうが精度がよいだろうか。
f(x)が1次関数のとき、どちらの式も正確な値を出してくれる。
では、2次関数f(x)=x²の場合はどうだろうか?
f'(a)=2aだから、(B1)式は正確な値を計算してくれるけれど、(A1)式による近似値はhという誤差をもっている。だから、(B1)の方がよい近似式なのだろうと推測できる。
近似式の誤差を判定する場合、o形式のテーラーの定理よりもO形式のものの方が適していると思うので、O形式のテーラーの定理をあらためて示す。
O形式のテーラーの定理
O形式のテーラーの定理より
これを(A1)に代入すると
一方、(B1)は、
を代入すると、
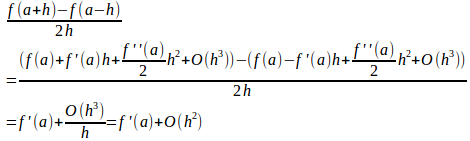
となる。
このことから、(A1)の誤差はh程度で(B1)の誤差はh²程度となり、(B1)の方が精度のよい近似式であると判定できる。
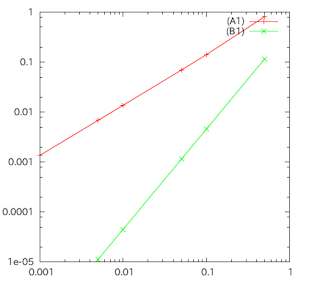 右のグラフは、
右のグラフは、とし、hの値を変化させ、(A1)と(B1)を用いてf'(1)=eを計算したときの誤差とhの関係を表したものである。横軸にはh、縦軸には誤差をとり、それを対数グラフであらわしてある。
このグラフを見ると、(B1)の方が(B1)よりも誤差が小さく、いい近似であることがわかる。
また、(A1)で計算した誤差とhの直線(?)の勾配が約1で誤差がhに比例し、(B1)の直線(?)の勾配が約2で誤差がh²に比例している。
このことからO(h)、O(h²)の意味が直感的に理解できるのではないだろうか。
ロピタルの定理の怪3 [ネコ騙し数学]
ロピタルの定理の怪3
定理A
f(x)、g(x)は点aを除く点aの近傍で微分可能でg'(x)≠0である。このとき、
で、かつ、が存在するならば、
が存在し、
である。
定理B
f(x)、g(x)は点aを除く点aの近傍で微分可能でg'(x)≠0である。このとき、
で、かつ、が存在するならば、
が存在し、
である。
定理Aを元にして定理Bを証明(?)してみようではないかというお話。
【定理Bの証明(?)】
だから
しかもだからaの十分近くではf(x)>0、g(x)>0で、f(x)≠0、g(x)≠0である。したがって、1/f(x)、1/g(x)は、aの十分近く(x≠a)で微分可能。
よって、ロピタルの定理Aより
である。
ここで、
これを⑨式に代入すると、
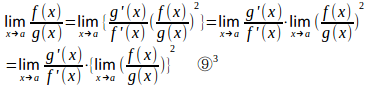
⑨³より、のとき
のとき、
だから、上と同様に考えて
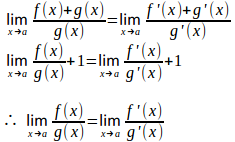
(Q.E.D.)
この証明が正しければ、難しいε-δ論法を使わない優れた証明です(^^)
数学の教科書の中には、
∞/∞の極限は、
だから、φ(x)=1/f(x)、ψ(x)=g(x)とおくと
と、0/0の極限に帰着させることができ、定理Aから云々
といった趣旨のことが書かれているものがあるとかないとか。
おそらく、上の証明(?)は、こうした方針のもとでなされたものなのでしょう。
そして、この方針にしたがって次の問題を解こうとすると大変なことになる(^^)
問題 次の極限を求めよ。
【解】
これは∞/∞の極限だから
(・・?
確かに、
ではあるが、問題をより複雑化させている(^^)
それにしてもロピタルの定理は恐ろしい。そして、ロピタルの定理(使用)の闇は未だ深い!!
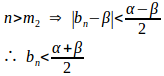
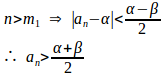
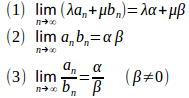
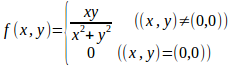
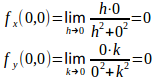
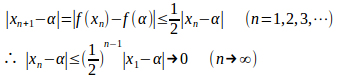
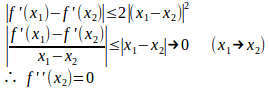
-graph.png)