番外編 不等式の証明

番外編　不等式の証明

いきなり、

これは次のように変形できるので、増加関数であることがわかる。

問題１　a、ｂが実数であるとき、次の不等式を証明せよ。

【証明】

　　
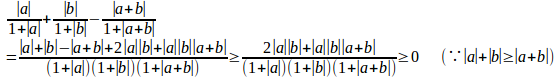
よって、

　　

である。

等号成立は、a=0またはb=0。

（証明終わり）

こんな計算はしたくない。

そこで、ずるをするにゃ。

　　

が増加関数であることを使って、証明することにする。

【ずるい証明】

　　

は増加関数。

|a|+|b|≧|a+b}だから

　　

また、

　　

①、②より

　　

である。

（証明終わり）

問題２　なるとき、との大小関係を調べよ。ただし、p>0、q>0、p+q=1とする。

x=yのとき、px+qy=x=yになるし、pf(x)+qf(y)=f(x)=f(y)になるので、pf(x)+qf(y)=f(px+qy)になる。次に、x≠yのときの大小関係の調べることにする。

しかし、面倒な計算はしたくないので、これから、ずるをするにゃ。

１年ほど前に、微分積分で凸関数というものをやった。凸関数は次のようなもの。

y=f(x)上の相異なる任意の２点をA(x,f(x))、B(y,f(y))とすると、この２点を結ぶ線分（弦）ABがこの曲線の弧ABよりも上にあるものを凸関数という。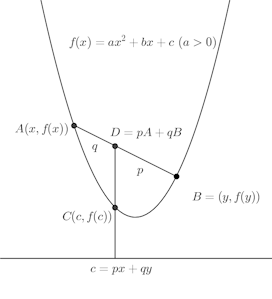

f(x)=ax²+bx+c（a>0）のときは、凸関数。で、p>0、q>0、p+q=1のとき、px+qyというのは、x軸上の(x,0)と(y,0)をq:pで分けた点と考えることができる。また、とすると、この点は線分ABをq;pに分ける点と考えられる。

Dは線分AB上にあるので、曲線上のよりも上にある。

したがって、a>0のとき、面倒くさい計算をするまでもなく、

　　

になる。a<0のときは、上下が逆転し、弦ABが線分ABの上に来るので、

　　

２次関数の図形的な意味を考えれば、計算をすることなく、大小関係を判定できるという話。

この問題の出題者は、このことを念頭にこの問題を作ったのだから、ケチをつけられる筋合いはない。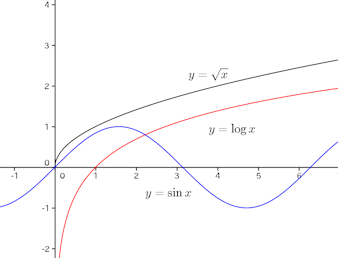



また、

　　

といった関数fは凹（上に凸）関数だから、
p>0、q>0、p+q=1のとき

　　

となるので、
　　

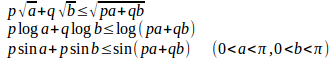
という不等式が得られる。

等号成立は、いずれの場合もa=b。

さり気なく、α≧0、β≧0とし,p=1/3、q=2/3とすると

　　

ここで、さらにさり気なくb≧0、c≧0とし

　　

さらに、もっとさり気なくa≧0、、α=a、β=(b+c)/2とし、この結果を⑨に放り込むと
　　

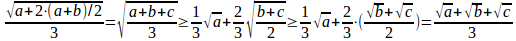
ここで、さらにもっと大胆に、a=x²、b=y²、c=z²とすると

　　

問題３　x、y、zを実数とするとき、次の問いに答えよ。

（１）　との大小を比較せよ。

（２）　a≧3のとき、x+y+z=x²+y²+z²=aを満たすx、y、zの値を求めよ。

（１）の不等式がどこから出てきたのかが、よく、わかる。これは関数の凸凹と深い関係があるんだケロ。
そして、

といった不等式も同様に得ることができる。

【解】

（１）　x+y+z<0のとき

　　

x+y+z≧0のとき
　　

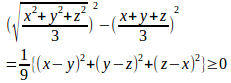
よって、

（２）　（１）より

また、x+y+z=x²+y²+z²=a≧3
　　

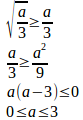
よって、a=3

また、a=3のとき①の右辺=左辺=1となり、x=y=zでなければならない。

よって、x=y=z=1である。